M1 BBS Math TD ACP
From silico.biotoul.fr
Contents |
Analyse en Composantes Principales
Récapitulatif de l'approche : M1 BBS ACP
Données utilisées
Dans ce TD, nous utilisons le jeu de données sur les iris. Description sur wikipedia http://en.wikipedia.org/wiki/Iris_flower_data_set
Et dans R, avec la commande
?iris
Chargement des données
d=iris[,1:4] # données numériques head(d) cl=iris[,5] # variétés d'iris (pour les couleurs notamment)
Affichage, recherche visuelle de corrélations
pairs(d, col=cl, pch=16)
Remarque : plot(d, col=cl, pch=16) permet d'obtenir le même graphique mais est moins explicite.
ACP avec la fonction princomp
Effectuer une ACP (non normée) à l'aide de la fonction princomp (et non prcomp qui utilise la décomposition en valeurs singulières au lieu des vecteurs propres et valeurs propres).
Afficher les individus projetés sur les 2 premiers axes.
Quelles sont les variances portées par ces axes ? Est-ce satisfaisant ?
Recalculer ces proportions à partir des valeurs propres et identifier les vecteurs propres dans ce que renvoie la fonction princomp.
Projection des individus dans le nouveau repère
Pour effectuer le changement de repère, c'est-à-dire de projeter les individus (lignes) dans le nouveau, il suffit d'utiliser le produit matriciel pour faire le produit de la matrice des coordonnées initiales U avec les vecteurs propres E : Uproj = UE
Effectuer la transformation et comparer le résultat avec le précédent.
La fonction princomp effectue un centrage des valeurs. Pour obtenir les mêmes échelles il faut donc soustraire la moyenne (des colonnes) à chaque valeur avant de faire la transformation.
Effectuer le centrage et la transformation et comparer.
ACP pas à pas
L'ACP consiste à projeter les individus dans un nouveau repère. La projection est obtenue à partir des vecteurs propres associés aux plus fortes valeurs propres de la matrice de variance-covariance des individus centrés. Les étapes consistent donc en :
- centrage des individus (comme précédemment)
- calcul de la matrice de variance-covariance des individus centrés
- calculs des valeurs propres et vecteurs propres de la matrice de variance-covariance
- projection pour obtenir les coordonnées (comme précédemment)
Effectuer les étapes ci-dessus et afficher le résultat. Comparer avec le résultat de princomp.
Obtenez-vous les mêmes variances portées par les axes ?
ACP normée avec princomp
Afin de ne pas accorder plus d’importance aux variables dont la variance est plus élevée, il faut généralement normaliser les valeurs.
Remarque : Cela revient à utiliser la matrice de correlation plutot que de variance-covariance.
Effectuer une ACP normée à l'aide de la fonction princomp.
Comparez les résultats avec et sans normalisation. Qu'observez-vous ?
ACP normée pas à pas
Pour faire une ACP normée, il est possible de travailler sur la matrice de corrélations.
Malheureusement, pour reproduire fidèlement les résultats de princomp, on ne peut pas utiliser la fonction cor car la formule utilisée pour la variance (et donc l'écart-type) est 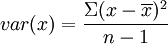 au lieu de
au lieu de 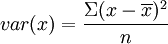 dans princomp (n étant le nombre de valeurs). Il faut donc le faire soi-même.
dans princomp (n étant le nombre de valeurs). Il faut donc le faire soi-même.
Pour centrer et réduire les valeurs, il faut donc appliquer la formule suivante : 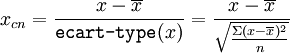
Effectuez vous-même la réduction des valeurs en utilisant n au lieu de n − 1 pour le calcul de la variance et de l'écart-type pour le calcul de la matrice des individus centrés réduits. Ensuite, vous pourrez effectuer les mêmes étapes que dans l'ACP pas à pas (utilisation de la matrice de variance-covariance).
Travail personnel
Refaire les analyses avec les packages mixOmics (http://mixomics.org/) et/ou ADE4 (https://cran.r-project.org/web/packages/ade4/index.html)
Liens
- Initiation à l'analyse en composantes principales réalisée par A. B. Dufour et J. R. Lobry