M1 Traitement de Donnees Biologiques - TP 3 R
From silico.biotoul.fr
m (→Tests statistiques) |
|||
| (3 intermediate revisions not shown) | |||
| Line 7: | Line 7: | ||
* Les tests d'homogénéité (comparaison de moyennes, comparaison de variances) | * Les tests d'homogénéité (comparaison de moyennes, comparaison de variances) | ||
| - | <span style='color: #990000'>ATTENTION: pour chaque test statistique, il est crucial de bien connaître l'hypothèse nulle du test ( | + | <span style='color: #990000'>ATTENTION : pour chaque test statistique, il est crucial de bien connaître l'hypothèse nulle du test (H<sub>0</sub>) pour pouvoir correctement interpréter !</span> |
| - | <span style='color: #990000'>Créez tout d'abord un répertoire de travail sur le bureau (par exemple TDB-TP3) et commencez par télécharger le fichier source que vous allez utiliser et compléter pour générer le compte rendu de TP : [[Media:M1.TDB.TP_tests_R.Rmd|M1.TDB.TP_tests_R.Rmd]] (click droit de la souris -- enregistrer la cible sous...).</span> Ouvrez le logiciel RStudio et chargez ce fichier puis lancez sa compilation pour voir le compte rendu. Pour cela cliquez sur le bouton Knit HTML ou bien utilisez la combinaison de touches Ctrl + shift + K. | + | <span style='color: #990000'>Créez tout d'abord un répertoire de travail sur le bureau (par exemple TDB-TP3) et commencez par télécharger le fichier source que vous allez utiliser et compléter pour générer le compte rendu de TP : [[Media:M1.TDB.TP_tests_R.Rmd|M1.TDB.TP_tests_R.Rmd]] (click droit de la souris -- enregistrer la cible sous...).</span> Ouvrez le logiciel RStudio et chargez ce fichier puis lancez sa compilation pour voir le compte rendu. Pour cela cliquez sur le bouton Knit HTML ou bien utilisez la combinaison de touches <tt>Ctrl + shift + K</tt>. |
= Tests de Chi2 = | = Tests de Chi2 = | ||
| Line 18: | Line 18: | ||
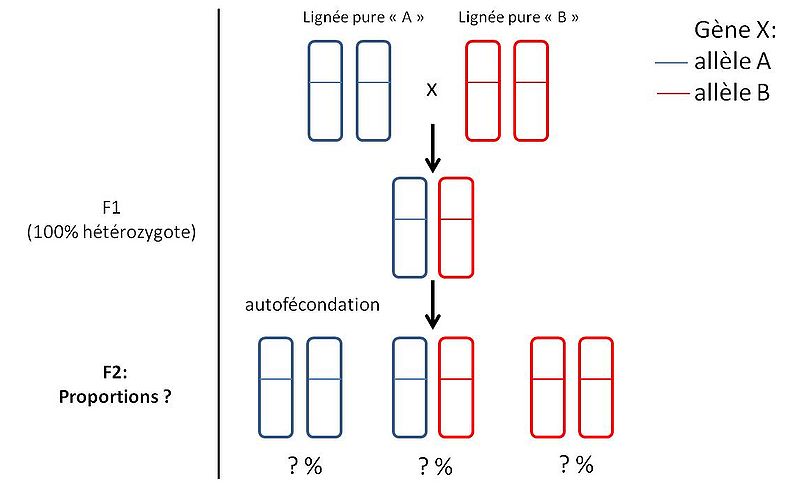
Notre exemple porte sur les proportion mendéliennes dans une descendance issue d'autofécondation d'une F1 hétérozygote. | Notre exemple porte sur les proportion mendéliennes dans une descendance issue d'autofécondation d'une F1 hétérozygote. | ||
| - | [[Image:mendel.jpeg]] | + | |
| + | [[Image:mendel.jpeg|800px]] | ||
Pour un gène avec 2 allèles, les proportions génotypiques attendues (relatives) dans la descendance sont: | Pour un gène avec 2 allèles, les proportions génotypiques attendues (relatives) dans la descendance sont: | ||
<source lang='rsplus'> | <source lang='rsplus'> | ||
| - | freq_exp =c(?,?,?) # mettre sous forme de fréquences relatives | + | freq_exp = c(?,?,?) # mettre sous forme de fréquences relatives |
</source> | </source> | ||
| - | Suite à un croisement effectué en laboratoire, les proportions génotypiques observées (absolues) parmis 100 individus descendants sont: | + | Suite à un croisement effectué en laboratoire, les proportions génotypiques observées (absolues) parmis 100 individus descendants sont : |
<source lang='rsplus'> | <source lang='rsplus'> | ||
| - | freq_obs =c(22,53,25) | + | freq_obs = c(22,53,25) |
</source> | </source> | ||
| - | Question: les proportions observées sont-elles conformes aux proportions mendéliennes? Pour cela il faut effectuer la commande suivante, et répondre aux questions ci-après: | + | Question : les proportions observées sont-elles conformes aux proportions mendéliennes? Pour cela il faut effectuer la commande suivante, et répondre aux questions ci-après : |
<source lang='rsplus'> | <source lang='rsplus'> | ||
| - | chisq.test(freq_obs,p=freq_exp) | + | chisq.test(freq_obs, p=freq_exp) |
</source> | </source> | ||
| Line 39: | Line 40: | ||
* La p-valeur est-elle inférieure ou supérieure au seuil alpha = 5% ? | * La p-valeur est-elle inférieure ou supérieure au seuil alpha = 5% ? | ||
| - | Conclusion: | + | Conclusion : |
<span style='color: #990000;'>Ajoutez ces parties à votre compte rendu.</span> | <span style='color: #990000;'>Ajoutez ces parties à votre compte rendu.</span> | ||
| Line 48: | Line 49: | ||
Le test de Chi2 d'indépendance s'effectue sur les effectifs des différentes classes des 2 variables qualitatives. | Le test de Chi2 d'indépendance s'effectue sur les effectifs des différentes classes des 2 variables qualitatives. | ||
| - | Notre exemple: la résistance ou sensibilité à un pathogène est-elle indépendante de l'écotype d'''Arabidopsis thaliana'' ? Autrement dit y | + | Notre exemple : la résistance ou sensibilité à un pathogène est-elle indépendante de l'écotype d'''Arabidopsis thaliana'' ? Autrement dit y a-t-il indépendance entre phénotype et écotype ? |
On va faire un test de Chi2, sur table de contingence des effectifs des différents écotypes pour chaque modalité du phénotype qualitatif, comme celle-ci : | On va faire un test de Chi2, sur table de contingence des effectifs des différents écotypes pour chaque modalité du phénotype qualitatif, comme celle-ci : | ||
| Line 56: | Line 57: | ||
Sensible 0 19 16 | Sensible 0 19 16 | ||
| - | Pour cela on crée un tableau de contingence : | + | Pour cela, on crée un tableau de contingence : |
<source lang='rsplus'> | <source lang='rsplus'> | ||
| - | mat=matrix(c(15,5,3,0,19,16),nrow=2,byrow=T, dimnames=list(c("R","S"), c("Col","Ws","Can"))) | + | mat = matrix( c( 15,5,3,0,19,16) , nrow=2 , byrow=T , dimnames=list( c("R","S"), c("Col","Ws","Can") ) ) |
mat | mat | ||
</source> | </source> | ||
| Line 64: | Line 65: | ||
Puis on utilise la commande : | Puis on utilise la commande : | ||
<source lang='rsplus'> | <source lang='rsplus'> | ||
| - | chisq.test(mat, correct =F) | + | chisq.test(mat, correct=F) |
</source> | </source> | ||
| Line 123: | Line 124: | ||
== Test d'homogénéité des variances (H0 = "les variances sont égales") == | == Test d'homogénéité des variances (H0 = "les variances sont égales") == | ||
| - | <span style='color: #990000;'>Test de | + | <span style='color: #990000;'>Test de Fisher</span> |
<source lang='rsplus'> | <source lang='rsplus'> | ||
var.test(Col_0,Mut_X1) | var.test(Col_0,Mut_X1) | ||
Revision as of 10:57, 30 September 2019
Contents |
Tests statistiques
La plupart des tests statistiques courants (et bien d’autres) sont programmés dans R. Dans ce TP, nous allons aborder quelques types de tests statistiques très courants :
- Les tests de χ2 (test de conformité, test d'indépendance), basés sur les effectifs de différentes classes
- Les tests d'adéquation (ici nous verrons l'adéquation à la loi Normale)
- Les tests d'homogénéité (comparaison de moyennes, comparaison de variances)
ATTENTION : pour chaque test statistique, il est crucial de bien connaître l'hypothèse nulle du test (H0) pour pouvoir correctement interpréter !
Créez tout d'abord un répertoire de travail sur le bureau (par exemple TDB-TP3) et commencez par télécharger le fichier source que vous allez utiliser et compléter pour générer le compte rendu de TP : M1.TDB.TP_tests_R.Rmd (click droit de la souris -- enregistrer la cible sous...). Ouvrez le logiciel RStudio et chargez ce fichier puis lancez sa compilation pour voir le compte rendu. Pour cela cliquez sur le bouton Knit HTML ou bien utilisez la combinaison de touches Ctrl + shift + K.
Tests de Chi2
Tests de Chi2 de conformité
On cherche à tester la conformité d'une (ou plusieurs) valeur(s) par rapport à une (des) valeur(s) standard(s) (ou théoriques). Le test de Chi2 de conformité s'effectue sur les effectifs des différentes classes d'une variable qualitative (ou quantitative).
Notre exemple porte sur les proportion mendéliennes dans une descendance issue d'autofécondation d'une F1 hétérozygote.
Pour un gène avec 2 allèles, les proportions génotypiques attendues (relatives) dans la descendance sont:
freq_exp = c(?,?,?) # mettre sous forme de fréquences relatives
Suite à un croisement effectué en laboratoire, les proportions génotypiques observées (absolues) parmis 100 individus descendants sont :
freq_obs = c(22,53,25)
Question : les proportions observées sont-elles conformes aux proportions mendéliennes? Pour cela il faut effectuer la commande suivante, et répondre aux questions ci-après :
chisq.test(freq_obs, p=freq_exp)
- Quelle est l'hypothèse nulle (H0) du test ? L'hypothèse alternative (H1) ?
- Qu'indique la p-valeur ?
- La p-valeur est-elle inférieure ou supérieure au seuil alpha = 5% ?
Conclusion :
Ajoutez ces parties à votre compte rendu.
Tests de Chi2 d'indépendance
On cherche à évaluer la relation entre deux variables qualitatives à 2 ou > 2 modalités. Le test de Chi2 d'indépendance s'effectue sur les effectifs des différentes classes des 2 variables qualitatives.
Notre exemple : la résistance ou sensibilité à un pathogène est-elle indépendante de l'écotype d'Arabidopsis thaliana ? Autrement dit y a-t-il indépendance entre phénotype et écotype ?
On va faire un test de Chi2, sur table de contingence des effectifs des différents écotypes pour chaque modalité du phénotype qualitatif, comme celle-ci :
Col Ws Can
Résistant 15 5 3
Sensible 0 19 16
Pour cela, on crée un tableau de contingence :
mat = matrix( c( 15,5,3,0,19,16) , nrow=2 , byrow=T , dimnames=list( c("R","S"), c("Col","Ws","Can") ) ) mat
Puis on utilise la commande :
chisq.test(mat, correct=F)
Conclusion (posez vous les mêmes questions que dans l'exercice précédent) ?
S'il y a une relation entre phénotype et écotype, comment se traduit-elle ?
obs=chisq.test(mat, correct =F)$observed exp=chisq.test(mat, correct =F)$expected obs-exp
Conclusion ?
Ajoutez ces parties à votre compte rendu.
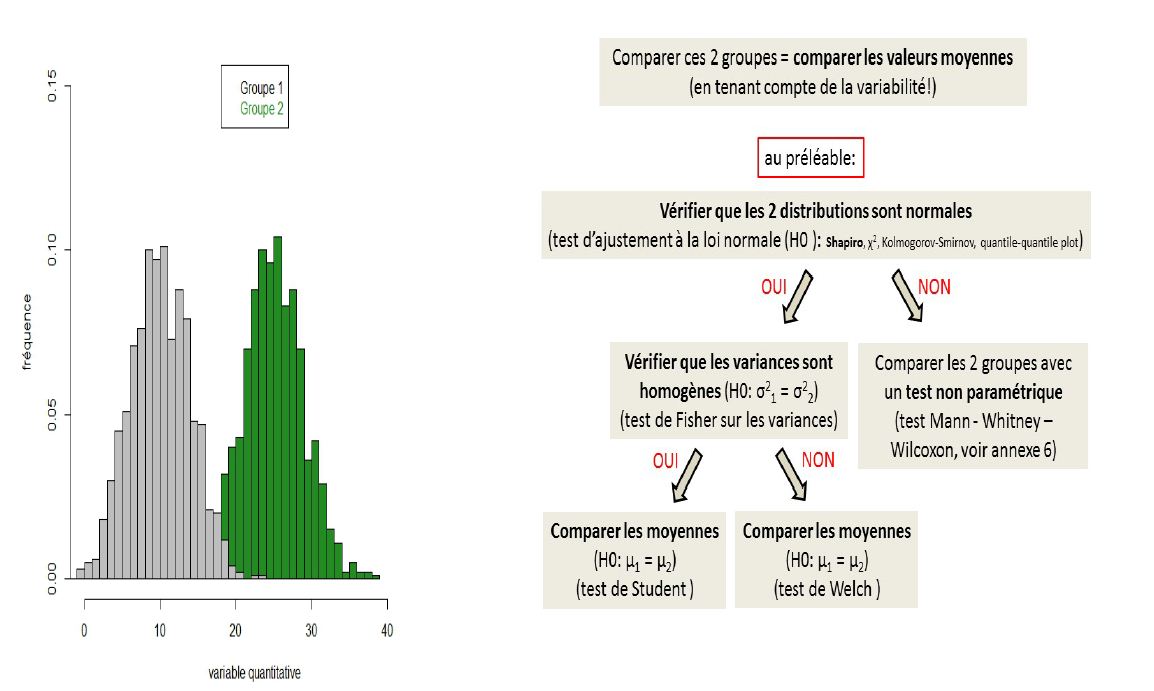
Tests paramétriques d'adéquation et tests d'homogénéité (sur une variable quantitative)
Nous allons intégrer ces tests dans le contexte d'une même analyse statistique.
Dans cet exercice, nous allons chercher à comparer les valeurs d'une variable quantitative mesurée dans 2 échantillons 1 et 2, à l'aide d'un test de Student de comparaison de moyennes de 2 échantillons. La question posée est : la taille moyenne (à un temps de donné) de plantules d' A. thaliana de génotype "sauvage" (Col_0) et d'un mutant pour le gène X1 (Mut_X1) est-elle la même (hypothèse H0) ?
Rappel de la procédure (vue en cours) :
Les données (petits calculs et graphiques)
# Vecteurs des tailles des plantes Col_0=c(4.30,4.25,3.50,3.35,4.30,3.75,3.55,4.10,3.95,4.55,4.25,3.75,3.85,4.15,3.55,4.75,3.95,3.65) Mut_X1=c(3.06,4.05,3.95,3.40,3.80,3.95,3.65,4,3.85,3.95,3.65,3.75,3.4)
# Valeurs moyennes mean(Col_0) mean(Mut_X1)
# Représentation graphique des données boxplot(Col_0,Mut_X1,names=c("Col_0","Mut_X1"),col=c("white","darkgreen"),ylab="taille (cm)") abline(h=mean(Col_0),col="black",lty=3,lwd=2) abline(h=mean(Mut_X1),col="green",lty=3,lwd=2) legend("topright", legend = c("Mut_X1","Col_0" ), text.col = c("darkgreen","black"))
Test d'adéquation à la loi normale (H0 = "les données suivent la loi Normale")
Test de Shapiro
shapiro.test(Col_0) shapiro.test(Mut_X1)
Conclusion ?
Test d'homogénéité des variances (H0 = "les variances sont égales")
Test de Fisher
var.test(Col_0,Mut_X1)
Conclusion ?
Test d'homogénéité (de comparaison) des moyennes (H0 = "les moyennes sont égales")
Test de Student bilatéral (H1 : "il y a une différence de moyenne entre Col_0 et Mut_X1")
# dans la commande t.test on peut spécifier si les variances des échantillons sont égales (var.equal=T) ou non(var.equal=F) # l'hypothèse alternative est "two.sided" par défaut t.test(Col_0,Mut_X1,var.equal = T)
Test de Student unilatéral (H1 = "la moyenne de Col_0 > (ou <) à la moyenne de Mut_X1")
# dans la commande t.test, on va spécifier l'hypothèse alternative: alternative = "greater" ou "less". Quel terme allez-vous mettre? t.test(Col_0,Mut_X1,var.equal = T, alternative = "???")
Conclusion finale ?
Ajoutez ces parties à votre compte rendu.
Test non paramétriques d'homogénéité (sur une variable quantitative)
Si les données ne suivent pas la loi Normale dans chaque échantillon, nous pouvons effectuer le test non paramétrique de Mann & Whitney
Dans cet exercice, nous cherchons à comparer l'expression d'un gène de défense chez la plante en condition d'infection par un microorganisme pathogène foliaire, avec la condition "contrôle" (plante non infectée).
Les données
Les données sont les valeurs d'expression normalisée du gène pour 3 réplicats techniques sur 3 réplicats biologiques de tissus foliaire.
non_infected=c(0.021,0.15,0.023,0.03,0.022,0.05,0.035,0.1,0.03) infected=c(1.22,1.12,1.06,1.04,0.86,1.24,1.96,0.9,2.5) mean(non_infected) mean(infected)
Test d'adéquation à la loi normale
# Test de Shapiro shapiro.test(infected) shapiro.test(non_infected)
Test non paramétrique d'homogénéité
# Test de Mann & Whitney (équivalent non paramétrique du test de Student) wilcox.test(infected,non_infected) # bilatéral wilcox.test(infected,non_infected,alternative="greater") # unilatéral
Conclusion?
Ajoutez tout cela au compte rendu de TP avant de l'envoyer à votre enseignant par mail (bonhomme@lrsv.ups-tlse.fr ou barriot@biotoul.fr). Le compte rendu est à envoyer avant de commencer le TP4. Envoyez les 2 fichiers (.Rmd et .html). Envoyez-vous aussi le mail en copie pour pouvoir vérifier que tout est bien passé. Mettez un titre tel que "Compte rendu TP3 TDB de -et votre Nom et Prénom-".
Liens
- Site de R : http://www.r-project.org et sites miroirs (dont ceux en France) pour télécharger le logiciel et les librairies : https://cran.r-project.org/mirrors.html
- RStudio : https://www.rstudio.com