M1 MABS BBS Math TD Modelisation
From silico.biotoul.fr
Contents |
Prise en main de la librairie deSolve
Nous allons commencer par modéliser des boucles de régulations de l'expression de gènes à partir d'exemples théoriques simplifiés à l'extrême.
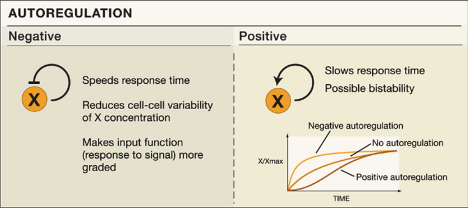
Tout d'abord, vous avez ci-contre le schéma d'une auto-régulation positive ou négative avec la concentration (X/Xmax) ou quantité de produit de X en fonction du temps.
Pour le modèle d'autorégulation positive, nous aurons comme variable d'état du système X : la concentration de l'espèce moléculaire X, et donc comme début de script :
library(deSolve) # chargement de la librairie state = c( X=0.1 )
Ensuite la variation de concentration de X dépend de la différence entre la quantité produite et la quantité dégradée. Pour faire simple, les paramètres, sous forme de vecteur dont les éléments sont nommés, sont les suivants :
- v la vitesse de synthèse
- auto une constante d'auto-régulation
- degradation la vitesse de dégradation
Ainsi, nous obtenons l'équation suivante :
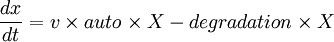
Les paramètres, là aussi sous forme de vecteur, sont définis de la manière suivante :
parameters = c( v = 0.04, degradation = 0.02, auto = 0.8 )
Et les équations sous forme de fonction R avec comme paramètres timelapse : le temps ; state : l'état du système ; et parameters : les paramètres du système
autoregulation = function(timelapse, state, parameters) { with(as.list(c(state, parameters)),{ dX = v * auto * X - degradation * X ## list(c(dX)) # liste renvoyée par la fonction }) }
Il n'y a plus qu'à effectuer une simulation du système et observer les résultats :
timelapse=1:200 # durée de la simulation sim1 <- ode(y = state, times = timelapse, func = autoregulation, parms = parameters) head(sim1) tail(sim1) plot(sim1, xlab = "times", ylab = "X") plot(timelapse, sim1[,'X']/max(sim1[,'X']), type='l', xlab='time', ylab='X/Xmax') # plot avec en ordonnées X/Xmax
Vous devriez obtenir le résultat suivant :
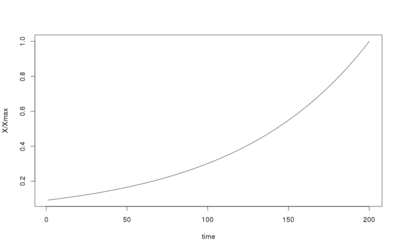
Effectuons à présent le même travail pour une boucle d'auto-régulation négative. Pour cela, considérons v comme la vitesse maximale de synthèse ; cette vitesse sera d'autant plus facilement atteinte que la concentration de X est faible, d'où :
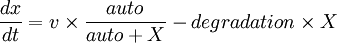
Modifier la fonction préalable et effectuer la simulation. Vous devriez obtenir le graphique suivant (avec en bleu la courbe précédente et en noir la courbe correspondant à une régulation négative) :
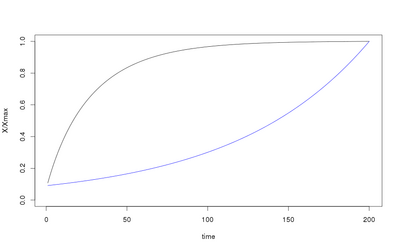
Autre exemple : boucle de régulation négative
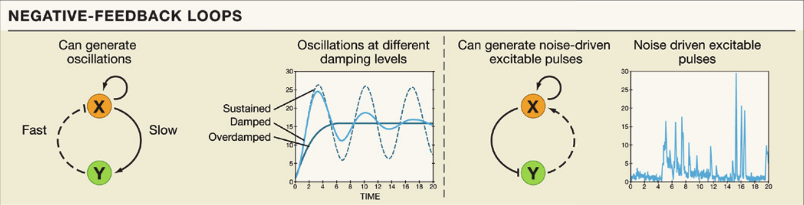
Nous allons nous intéresser maintenant au circuit ci-contre (circuit de gauche) :
Dans ce circuit, X s'auto-régule positivement et active également Y, mais plus lentement (que lui-même X). Y, quant à elle, réprime X, de manière rapide, par exemple en stimulant la dégradation de X.
On pourra obtenir les équations (ultra simplifiées) suivantes :
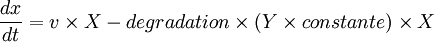
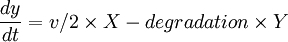
avec comme paramètres :
- v: la vitesse de synthèse (et v/2 pour une activation lente de Y)
- degradation: la vitesse de dégradation
On obtient donc le script suivant pour le scénario "damped oscillations" :
timelapse=1:2000 parameters = c( v = 1, degradation = 0.01 ) state = c(X=0.10, Y = 0.10) nfl = function(t, state, parameters) { with(as.list(c(state, parameters)),{ dX = v * X - degradation*(Y*10) * X dY = v/2 * X - degradation * Y ## list(c(dX, dY)) }) } sim2 <- ode(y = state, times = timelapse, func = nfl, parms = parameters); X = sim2[,'X'] ; Y = sim2[,'Y'] plot(timelapse, X, t='l', ylim= c(min(X,Y), max(X,Y)), col='red', ylab='') lines(timelapse, Y, col='blue')
qui produit le résultat suivant :
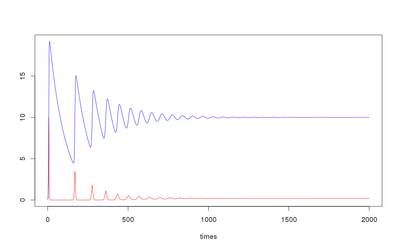
Système continu : Modèle de rythme circadien de cyanobactérie
Travail basé sur la publication A Model for the Circadian Rhythm of Cyanobacteria that Maintains Oscillation without Gene Expression de Kurosawa et al..
Dans ce travail, ils proposent un modèle de régulation de la phosphorylation de la protéine KaiC capable de générer des oscillations circadiennes chez les cyanobactéries. Nous allons ici implémenter leur système et vérifier certains de leurs résultats.
L'état du système est le suivant :
- la protéine KaiA se trouve sous 2 formes : KaiA (inactive) et Kai* (active)
- la protéine KaiC également : KaiC et KaiC-P (phosphorylée)
- la protéine KaiB aussi : KaiB (inactive) et KaiB* (active)
Le système évolue :
- KaiA* stimule la phosphorylation de KaiC
- KaiB* stimule la déphosphorylation de KaiC
- KaiC-P stimule l'inactivation de KaiB. L'activité de KaiB dépend de sa localisation et éventuellement de plusieurs formes chimiques de KaiB (comme pour KaiC).
Cela correspond à la figure 3C de la publication :
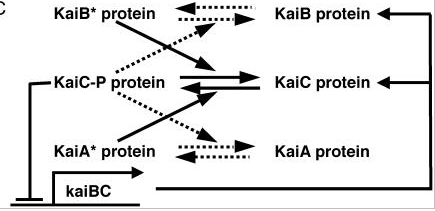
Ceci se traduit par les équations 1,2 et 3 de la publication.
Pour x, la quantité de de KaiC-P, avec :
- p et a : la vitesse de phosphorylation de KaiC
- C0 et s: la concentration initiale de KaiC et sa variation de concentration, donc C0s - x la quantité de KaiC non phosphorylée
- b (y+f) : la vitesse de déphosphorylation de KaiC-P par KaiB*
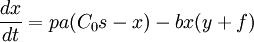
Pour y, la quantité de KaiB* (KaiB active), avec :
- g : vitesse d'activation de KaiB
- k1xn / (qn + xn) : la désactivation de KaiB* par kaiC-P
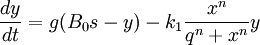
Les variations de concentration de KaiB totale et KaiC totale sont données dans l'équation 2, avec :
- ε1: constante permettant d'ajuster les vitesse de synthèse et de dégradation
- λ: la vitesse de transcription
- μ: la vitesse de décomposition
- la transcription de kaiBC est inhibée par la concentration en KaiC-P, d'où la vitesse de transcription:
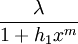
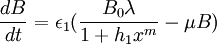
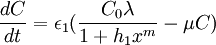
En synthétisant ces différentes équations et en remplaçant dans l'équation 1 C0s par C et B0s par B, on obtient le système suivant :
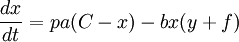
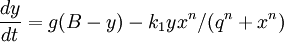
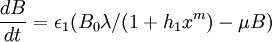
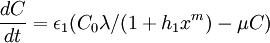
Les valeurs des paramètres et concentration initiale pour obtenir la figure 4B sont fournis dans la légende des figures 2A et 4A, et 4B pour epsilon1.
Vous devriez obtenir les courbes suivantes :
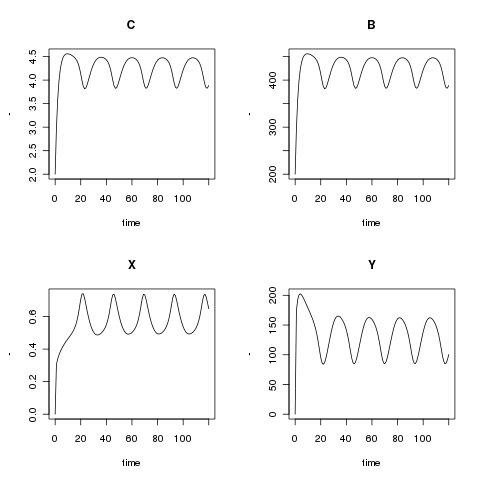 et
et 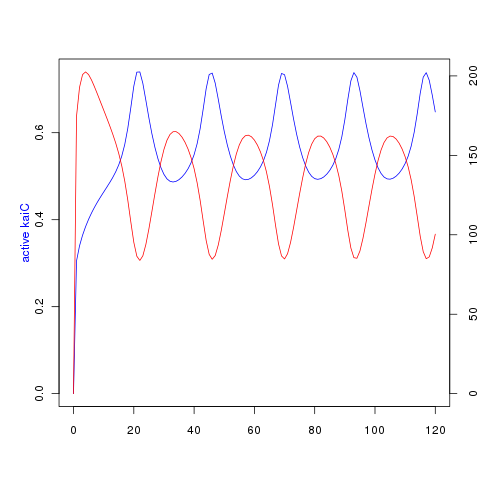
Exercice pour chez soi. Système discret : plantes annuelles
Les plantes annuelles tirent leur nom du fait qu'elles vivent moins d'un an. Elles effectuent leur cycle de vie en une seule année et passent l'hiver uniquement sous forme de graines. Nous allons nous intéresser à l'élaboration d'un modèle pour l'étude du développement et de la prolifération de ces plantes.
Description du cycle
Les graines germent en mai pour donner des plantes. Ces plantes fleurissent et produisent des graines qui sont dispersées à partir d'août. Une partie des graines sont infectées par divers pathogènes et meurent ou bien sont consommées par différents animaux pendant l'hiver. L'année suivante, le cycle recommence : une partie des graines germent, ... Les graines n'ayant pas germé attendront l'année suivante, si elles ne germent pas l'année suivante, elles ne germeront plus.
Paramètres du modèle
- γ : nombre de graines produites par une plante
- α : proportion de graines produites l'année précédente qui germent en mai
- β : proportion de graines d'il y a 2 ans qui germent en mai
- σ : proportion de graines qui survivent à l'hiver
Etat du système
En début d'année, l'état du système est donné par le nombre de graines de l'année précédente et d'il y a 2 ans.
Travail à réaliser
- Faire un schéma du système/cycle
- Identifier sur ce schéma les variables d'états qui vont être utilisées
- Écrire les relations liant les variables d'une année n à l'année suivante n + 1.
- Implémenter le modèle obtenu dans R avec la librairie deSolve. Pour cela, on utilisera les valeurs suivantes pour les paramètres :
- γ = 2
- α = 0.5
- β = 0.25
- σ = 0.8
- Effectuer une simulation, sur 20 ans à partir de 100 graines et d'un sol vierge
- Au bout de combien d'années n'a-t-on plus de plante en partant de 50 graines ?
- Déterminer le taux γ minimal nécessaire au maintient des plantes pour les paramètres précédents (sauf γ)
Remarque : pour les simulations, vous utiliserez comme précédemment la fonction ode(...) mais il faudra bien préciser le paramètre method dans le cadre de données discrètes (on "saute" de l'année n à l'année n+1 sans intermédiaire), donc : out = ode( ..., method='euler')