M1 MABS Graphes TP Parcours en largeur - Plus court chemin
From silico.biotoul.fr
(Difference between revisions)
m (→Plus court chemin - Bellman-Ford) |
m (→Plus court chemin - Bellman-Ford) |
||
| Line 41: | Line 41: | ||
'''Ajoutez''' la méthode à votre librairie et testez la sur le graphe [[File:M1MABS Graphe Bellman-Ford.tab]] à partir du sommet A. | '''Ajoutez''' la méthode à votre librairie et testez la sur le graphe [[File:M1MABS Graphe Bellman-Ford.tab]] à partir du sommet A. | ||
| - | Afin de gagner du temps, la méthode <tt> | + | Afin de gagner du temps, la méthode <tt>loadTAB</tt> vous est fournie : |
| + | <source lang='python'> | ||
| + | def loadTAB(self, filename): | ||
| + | """ | ||
| + | Loads a graph in Cytoscape tab format | ||
| + | Assumed input: | ||
| + | id1 id2 weight color ... | ||
| + | A B 6 blue ... | ||
| + | """ | ||
| + | with open(filename) as f: | ||
| + | # GET COLUMNS NAMES | ||
| + | tmp = f.readline().rstrip() | ||
| + | attNames= tmp.split('\t') | ||
| + | # REMOVES FIRST TWO COLUMNS WHICH CORRESPONDS TO THE LABELS OF THE CONNECTED VERTICES | ||
| + | attNames.pop(0) | ||
| + | attNames.pop(0) | ||
| + | # PROCESS THE REMAINING LINES | ||
| + | row = f.readline().rstrip() | ||
| + | while row: | ||
| + | vals = row.split('\t') | ||
| + | v1 = vals.pop(0) | ||
| + | v2 = vals.pop(0) | ||
| + | att = {} | ||
| + | for i in xrange(len(attNames)): | ||
| + | att[ attNames[i] ] = vals[i] | ||
| + | self.addEdge(v1, v2, att) | ||
| + | row = f.readline().rstrip() # NEXT LINE | ||
| + | </source> | ||
<!-- | <!-- | ||
Revision as of 16:18, 19 February 2015
Contents |
Parcours en largeur
Algorithme :
BFS(G, s) for each vertex uV(G) do color[u]
WHITE d[u]
π[u]
NIL color[s]
GRAY d[s]
0 Q
enqueue(Q, s) while Q
do u
dequeue(Q) for each vertex v
Adj[u] do if color[v] = WHITE then color[v]
GRAY d[v]
d[u] + 1 π[v]
u enqueue(Q, v) color[u]
BLACK
Charger le graphe de la séance précédente (File:M1MABS Graphe dressing.sif), et effectuer un parcours en largeur depuis sous-vetements.
Plus court chemin - Bellman-Ford
Rappel de l'algorithme:
INITIALIZE-SINGLE-SOURCE(G, s) for each vertex vV(G) do d[v]
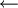
π[v]
NIL d[s]
0 RELAX(u, v, w) if d[v] > d[u] + w(u, v) then d[v] = d[u] + w(u,v) π[v]
u BELLMAN-FORD(G, w, s) INITIALIZE-SINGLE-SOURCE(G, s) for i
1 to |V(G)| - 1 do for each edge (u,v)
E(G) do RELAX(u, v, w)
Ajoutez la méthode à votre librairie et testez la sur le graphe File:M1MABS Graphe Bellman-Ford.tab à partir du sommet A.
Afin de gagner du temps, la méthode loadTAB vous est fournie :
def loadTAB(self, filename): """ Loads a graph in Cytoscape tab format Assumed input: id1 id2 weight color ... A B 6 blue ... """ with open(filename) as f: # GET COLUMNS NAMES tmp = f.readline().rstrip() attNames= tmp.split('\t') # REMOVES FIRST TWO COLUMNS WHICH CORRESPONDS TO THE LABELS OF THE CONNECTED VERTICES attNames.pop(0) attNames.pop(0) # PROCESS THE REMAINING LINES row = f.readline().rstrip() while row: vals = row.split('\t') v1 = vals.pop(0) v2 = vals.pop(0) att = {} for i in xrange(len(attNames)): att[ attNames[i] ] = vals[i] self.addEdge(v1, v2, att) row = f.readline().rstrip() # NEXT LINE
Plus courts chemins - Floyd-Warshall
Pour l'agorithme suivant,
- D[x,y] est la distance du plus court chemin entre les sommets x et y
- N[x,y] est le successeur de x dans le plus court chemin allant de x à y
- W[x,y] est la valuation de l'arc (x,y)
Algorithme :
initialiser D = W, et N
pour k de 1 à n
pour i de 1 à n
pour j de 1 à n
si D[i,k] + D[k,j] < D[i,j] alors
D[i,j] = D[i,k] + D[k,j]
N[i,j] = k
Récupération du plus court chemin à partir de la matrice N :
plusCourtChemin(D,N, i,j)
si D[i,j] est infinie alors
il n'y a pas de chemin entre i et j
chemin = initialiserChemin(i)
k = N[i,j]
tant que k est défini faire
ajouter(chemin, k)
k = N[k,j]
ajouter(chemin, j)
Implémenter les algorithmes ci-dessus en R et les tester sur la matrice suivante :
# adjacency matrix M=matrix( c(0,1,0,0,1,0,0,1,0,0,1,1,0,0,0,0), ncol=4, byrow=T) M # [,1] [,2] [,3] [,4] #[1,] 0 1 0 0 #[2,] 1 0 0 1 #[3,] 0 0 1 1 #[4,] 0 0 0 0 # test fw=FloydWarshall(M) fw #$distances # [,1] [,2] [,3] [,4] #[1,] 2 1 Inf 2 #[2,] 1 2 Inf 1 #[3,] Inf Inf 1 1 #[4,] Inf Inf Inf Inf # #$chemins # [,1] [,2] [,3] [,4] #[1,] 2 NA Inf 2 #[2,] NA 1 Inf NA #[3,] Inf Inf NA NA #[4,] Inf Inf Inf Inf FloydWarshallPath(fw, 1,4) #[1] 1 2 4
Extraire la grosse composante connexe de String au format sif puis transformer le fichier en matrice d'adjacence. Ensuite, sous R, charger la matrice et calculer le diamètre du graphe.