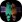M1 BBS Data Mining TD Classification
From silico.biotoul.fr
Introduction
Afin de mettre en pratique les concepts vus en cours, nous allons nous appuyer sur des jeux de données publiques hébergées par le UC Irvine Machine Learning Repository.
Pour le premier jeu de données intitulé "mushrooms", il s'agit de classer un champignon comme comestible ou non en fonction d'attributs de type catégoriel. Pour le second - italian wines -, il s'agit de prédire le cultivar du cépage en fonction de mesures quantitatives.
Pour cela, nous utiliserons différents environnements :
- KNIME : un logiciel d'analyse qui est en fait un environnement dérivé de la plateforme de développement intégré Eclipse
- R : environnement orienté calcul numérique & statistiques
- python : un langage de programmation afin de voir l'utilisation de bibliothèque de fouille de données ainsi que pour réaliser son propre programme de classification
Environnement de travail
Nous allons utiliser quelques librairies pas toujours présentes dans un environnement par défaut. C'est l'occasion de s'initier à la gestion de différents environnements de développement et/ou d'analyse. Pour cela, nous allons utiliser l'utilitaire conda. Plus d'informtaion sur cet utilitaire sur silico Conda ou sur gitlab via un projet dans lequel vous pouvez contribuer (envoyer un mail à R. Barriot avec votre identifiant gitlab, ex: @rbarriot pour R. Barriot).
Les commandes suivantes sont à exécuter dans un terminal (surtout PAS en tant qu'administrateur/root).
# dépôts des librairies et programmes conda config --add channels conda-forge conda config --add channels bioconda # création d'un nouvel environnement contenant les librairies spécifiées conda create -n fouille r-base r-tidyverse r-ggally r-reticulate r-rmysql bioconductor-made4 r-codetools r-caTools r-rprojroot r-shiny r-plotly r-knitr r-dt r-kableextra r-cluster r-gridextra r-caret r-e1071 python numpy pandas scipy scikit-learn matplotlib plotly ipykernel nb_conda_kernels jupyterlab auto-sklearn # activation de ce nouvel environnement conda deactivate && conda activate fouille
Classification
TP 2h - Classification par arbres de décision et évaluation des performances - données Mushrooms
Les données
Le premier jeu de données concerne des champignons. Il est publié à l'adresse : http://archive.ics.uci.edu/ml/datasets/Mushroom
La description du jeu de données est aussi accessible ici.
Le jeu de données modifié pour inclure une première ligne contenant les noms des colonnes est disponible là : Media:mushrooms.data.txt.
Analyses préliminaires avec R
Charger le jeu de données et utiliser la commande summary pour vous faire une idée du nombre d'instances de chaque classe, et du nombre de modalité de chaque facteur (attribut/dimension/variable).
Etudiez ensuite la liaison entre chaque variable et la classe. Pour cela, vous pourrez utiliser le test du χ2 d'indépendance. Utilisez également la fonction table (pour générer une table de contingence) pour la combiner avec la fonction plot afin d'explorer visuellement les biais entre chaque attribut et la classe.
Exemple de visualisation :
Ces analyses devrait vous permettre de vous faire une idée sur la pertinence d'un attribut en ce qui concerne l'objectif : classer un champignon comme comestible ou pas.
Quels attributs vous semblent les plus pertinents ?
A partir de là, il semble qu'aucun attribut peut permettre à lui seul de classer un échantillon. Nous allons donc utiliser des méthodes d'apprentissage proposées dans le logiciel KNIME.
Analyses avec KNIME
Pour cette partie, nous allons utiliser l'environnement pour la fouille de données KNIME. C'est un logiciel en Java développé à l'origine par l'université de Constance (Allemagne).
L'installation pour linux consiste à télécharger et désarchiver le contenu d'un fichier au format .tar.gz. Une copie de la dernière version a sûrement été placée sur le PC de l'intervenant : http://pc-bioinfo-01
Après extraction, il faudra lancer l'exécutable en ligne de commande qui se trouve dans le nouveau répertoire knime_VERSION/knime.
Construction du modèle
La première étape consiste à charger les données. Dans KNIME, ajoutez un noeud File Reader (section IO pour Input/Output) et configurez-le afin de charger le fichier de données.
Comme premier exercice, ajoutez un noeud Decision Tree Learner (induction d'arbre de décision) et connectez la sortie du File Reader à l'entrée du Decision Tree Learner. Configurez ce dernier pour qu'il cherche à prédire la classe du champignon. Lancez l'éxécution de ces noeuds et visualisez l'arbre de décision inféré. Quelles sont les variables les plus importantes ?
Remarque : A la configuration du noeud Decision Tree Learner, observez les autres paramètres disponibles (mesure de pertinence d'un attribut, élagage).
Effectuez la même chose avec un classificateur bayésien naïf et visualisez le modèle obtenu.
Evaluation des performances
Afin de décider quelle méthode fonctionne le mieux (arbre de décision ou bayésien naïf) pour ce jeu de données et avec quels paramètres (gain ratio ou gini index par exemple), vous allez effectuer des validation croisées.
Pour cela, ajoutez et en configurez un noeud Cross validation (section Meta). Une leave-one-out cross validation (ou LOOCV) sera pour ce TP trop couteuse en temps (> 8000 modèles inférés par méthode). Essayez par exemple avec les valeurs 3 et 10 pour le noeud X-partitioner (3-fold ou 10-fold cross validation). Ceci aura pour effet de diviser le jeu de données en entrées en jeux de données d'apprentissage (pour le learner) et jeux de données tests (pour le modèle produit par le learner). Configurez enfin le noeud X-agregator qui confrontera la classe prédite à la classe connue.
Examinez ensuite le taux d'erreurs à l'aide d'un noeud Statistics view.
Faites varier la méthode et ces paramètres et notez à chaque fois les performances obtenues (taux d'erreurs) :
- arbre de décision
- gain ratio ou gini index
- no pruning ou MDL
- bayésien naïf
Qu'observez vous lorsque vous augmentez le nombre de validations croisées (3-fold vs. 10-fold) ?
Saisie des résultats : https://docs.google.com/spreadsheets/d/1-jodQc1frwTepwzwAvTD7qi_zMwPsj5LfKI6B4qAJKE/edit?usp=sharing
TP 4h - Italian wines - R/tidyverse + LDA
Sujet déposé sur gitlab → https://gitlab.com/rbarriot/datamining/-/tree/master/tp.italian.wine.lda.tidyverse
TP 4h - Classificateur bayésien naïf - jupyterlab + pandas + script
Sujet déposé sur GitLab → https://gitlab.com/rbarriot/datamining/-/tree/master/tp.naive.bayes.jupyter-lab.pandas.script
TP 2h - Classificateur k plus proches voisins - modules python sklearn et auto-sklearn
Sujet sur le dépôt GitLab → https://gitlab.com/rbarriot/datamining/-/tree/master/tp.knn.jupyter.sklearn.autosklearn
Clustering
Italian wines - TP 4h - clustering
Objectfis : Mise en oeuvre des concepts vus en cours concernant l'évaluation des résultats d'un clustering.
Sujet sur le dépôt GitLab → https://gitlab.com/rbarriot/datamining/-/tree/master/tp.clustering