M1 BBS Graphes TP Librairie - Parcours de graphes
From silico.biotoul.fr
Librairie python pour le traitement de graphes
Vous allez réaliser un module python pour les graphes (orientés ou non) que vous allez construire au fur et à mesure de ce TP, du suivant, et du projet pour cette UE.
Ce module va permettre :
- le chargement d'un graphe sous différents formats (SIF et TAB vus précédemment, OBO pour la Gene Ontology et produits de gènes pour les annotations des gènes en GOTerm),
- le parcours en largeur (BFS),
- le parcours en profondeur (DFS),
- la détection de cycle/circuit,
- le tri topologique,
- l'identification des plus courts chemin à partir d'un sommet (Bellman-Ford), ou entre toutes les paires de sommets (Floyd-Warshall),
- ...
Structures de données et représentation d'un graphe
Pour commencer, il vous faut définir les structures de données que vous allez utiliser pour représenter et traiter des graphes. Un graphe
- peut avoir différents attributs (nom, ordre, diamètre, ...),
- peut être orienté ou non,
- peut être pondéré ou non,
- possède un ensemble de sommets,
- possède un ensemble d'arcs ou d'arêtes.
De plus, un sommet peut avoir différentes étiquettes ou attributs : identifiant, nom, index, date de passage, couleur, coordonnées (x,y), etc.. De même, un arc ou une arête peut avoir différents attributs : poids, longueur, couleur, type, etc..
Un des choix cruciaux va être de choisir la représentation (structure de données utilisée) pour les arcs ou arêtes (notés arcs par la suite) : il est possible, par exemple, d'opter pour une matrice d'adjacence ou des listes d'adjacence. Si l'on manipule des graphes peu denses, la représentation par listes d'adjacence est préférable.
Toutes ces informations peuvent être stockées dans un dictionnaire à l'allure suivante (avec la syntaxe python) :
graph = {
'directed': True,
'weighted': False,
'nodes': {},
'edges': {},
'weight_attribute': None,
}
Les clés nodes et edges pointent elles-mêmes vers des dictionnaires (imbriqués).
Considérons le graphe G très simple suivant constitué de 2 sommets et d'un arc (A,B) ayant un poids de 5 :
weight: 5 A -------------> B
Le plus compliqué est le stockage des arcs qui peuvent avoir différents attributs. Le choix proposé est d'utiliser un dictionnaire de dictionnaires de dictionnaires de dictionnaires ... : pour l'arc de A à B de poids 5 :
graph['edges']['A']['B']['weight'] = 5
En d'autres termes :
- graph['edges'] est un dictionnaire dont les clés sont les sommets source des arcs et dont les valeurs sont des dictionnaires,
- graph['edges']['A'] est un dictionnaire pour les arcs dont l'extrémité initiale est le sommet A. Ce sommet peut avoir un degré sortant supérieur à 1, donc il faut stocker les extrémités terminales sous forme de dictionnaire. Les clés de ce dictionnaire seront donc les sommets correspondants aux extrémités terminales des sommets dont l'extrémité initiale est A,
- graph['edges']['A']['B'] est un dictionnaire permettant de stocker les attributs de l'arc (A,B),
- graph['edges']['A']['B']['weight'] est ainsi le poids de l'arc A --> B.
Ainsi, si un graphe pondéré est chargé, on pourra choisir de stocker le poids des arcs dans les attributs des arcs (accessibles à partir de la clé edges) avec la clé weight. Pour G, le dictionnaire pour son stockage aura l'allure suivante :
g = { 'directed': True, 'weighted': True, 'nodes': { 'A': { }, 'B': { } }, 'edges': { 'A': { 'B': { 'weight': 5 } } }, 'weight_attribute': 'weight' }
Pour créer un graphe, le module python que vous allez développer devrait donc commencer par le code python suivant :
#!/usr/bin/env python from pprint import pprint # pour afficher de manière plus lisible des dictionnaires imbriqués import numpy as np # for Floyd-Warshall matrices # functions ########### def create_graph(directed = True, weighted = False, weight_attribute=None): g = { 'nodes': {}, 'edges': {}, 'directed': directed, 'weighted': weighted, 'weight_attribute': weight_attribute } return g ########### # Tests def TP1_tests(): pprint('#### create_graph ####') g = create_graph() pprint(g) def TP2_tests(): g = load_SIF('dressing.sif') pprint(g) p = BFS(g, 'sous-vetements') pprint(p) ############# # Perform tests if not imported by another script if __name__ == "__main__": TP1_tests() # TP2_tests()
Créez le fichier correspondant à votre librairie (par exemple Graph.py) et testez-le.
Il s'agit maintenant de pouvoir ajouter des sommets et des arcs.
Avant d'ajouter un sommet, il faut s'assurer qu'il n'existe pas déjà :
def add_node(g, n, attributes = None): # TP1 if n not in g['nodes']: # ensure node does not already exist if attributes is None: # create empty attributes if not provided attributes = {} g['nodes'][n] = attributes g['edges'][n] = {} # init outgoing edges return g['nodes'][n] # return node attributes
De même, pour ajouter un arc, il faut
- s'assurer que l'extrémité initiale existe
- s'assurer que l'extrémité terminale existe
- s'assurer que l'arc n'existe pas
- si le graphe n'est PAS orienté, il faut ajouter A --> B et B --> A
def add_edge(g, n1, n2, attributes = None, n1_attributes = None, n2_attributes = None): # TP1 # create nodes if they do not exist if n1 not in g['nodes']: add_node(g, n1, n1_attributes) # ensure n1 exists if n2 not in g['nodes']: add_node(g, n2, n2_attributes) # ensure n2 exists # add edge(s) only if they do not exist if n2 not in g['edges'][n1]: if attributes is None: # create empty attributes if not provided attributes = {} g['edges'][n1][n2] = attributes if not g['directed']: g['edges'][n2][n1] = g['edges'][n1][n2] # share the same attributes as n1->n2 return g['edges'][n1][n2] # return edge attributes
Chargement d'un fichier au format SIF : il s'agit de
- créer un graphe (orienté ou non, mais pas pondéré)
- lire le fichier ligne par ligne, et pour chacune des lignes : ajout des sommets et des arcs
def load_SIF(filename, directed=True, column_separator='\t'): # TP1 # line syntax: nodeD <relationship type> nodeE nodeF nodeB g = create_graph(directed) # new empty graph with open(filename) as f: # OPEN FILE # PROCESS THE REMAINING LINES row = f.readline().rstrip() # read next line and remove ending whitespaces while row: vals = row.split(column_separator) # split line on the specified column separator (defaults to tab) for i in range(2, len(vals)): att = { 'type': vals[1] } # set edge type add_edge(g, vals[0], vals[i], att) row = f.readline().rstrip() # read next line return g # return graph
Vous pourrez tester ces fonctions sur le fichier File:M1BBS Graphe dressing.sif avec la fonction suivante :
def TP1_tests(): print('#### create_graph ####') g = create_graph() pprint(g) print('## Adding node A') add_node(g,'A') pprint(g) print('## Adding edge A -> B') add_edge(g, 'A', 'B') pprint(g) print('## #Loading SIF file dressing.sif') g = load_SIF('dressing.sif') pprint(g)
Parcours en largeur
Algorithme :
BFS(G, s) for each vertex uV(G) do color[u]
WHITE d[u]
π[u]
NIL color[s]
GRAY d[s]
0 Q
enqueue(Q, s) while Q
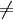
do u
dequeue(Q) for each vertex v
Adj[u] do if color[v] = WHITE then color[v]
GRAY d[v]
d[u] + 1 π[v]
u enqueue(Q, v) color[u]
BLACK
Charger le graphe utilisé dressing.sif, et effectuer un parcours en largeur depuis sous-vetements.
Si vous n'êtes pas trop en retard sur l'avancement du TP : Quels sont les sommets que l'on peut atteindre à partir de wbbJ dans le graphe que vous avez filtré (neighborhood, coexpression et experimental >= 800) ? Vous aurez besoin pour cela d'utiliser la fonction load_TAB qui vous est fournie ci-dessous.
def load_TAB(filename, directed=True, weighted=False, weight_attribute=None, column_separator='\t'): """ parse a TAB file (as cytoscape format) and returns a graph. line syntax: id1 id2 att1 att2 att3 ... """ g = create_graph(directed, weighted) with open(filename) as f: # GET COLUMNS NAMES tmp = f.readline().rstrip() attNames= tmp.split(column_separator) # REMOVES FIRST TWO COLUMNS WHICH CORRESPONDS TO THE LABELS OF THE CONNECTED VERTICES attNames.pop(0) # remove first column name (source node not to be in attribute names) attNames.pop(0) # remove second column (target node ...) # PROCESS THE REMAINING LINES row = f.readline().rstrip() while row: vals = row.split(column_separator) v1 = vals.pop(0) v2 = vals.pop(0) att = {} for i in range(len(attNames)): att[ attNames[i] ] = vals[i] add_edge(g, v1, v2, att) row = f.readline().rstrip() # NEXT LINE return g
Parcours en profondeur et applications
Implémentez et testez ensuite le parcours en profondeur dont on vous rappelle l'algorithme :
DFS(G) for each vertex uV(G) do color[u]
WHITE pred[u]
NIL time
0 for each vertex u
V(G) do if color[u] = WHITE then DFS-VISIT(u) DFS-VISIT(u) color[u]
GRAY time
time + 1 d[u]
time for each vertex v
Adj[u] do if color[v] = WHITE then pred[v]
u DFS-VISIT(v) class[ (u,v) ]
TREE EDGE else if color[v] = GRAY then class[ (u,v) ]
BACK EDGE else if d[u] > d[v] then class[ (u,v) ]
CROSS EDGE else class[ (u,v) ]
FORWARD EDGE color[u]
BLACK time
time + 1 f[u]
time
Implémentez et testez la fonction is_acyclic() qui renvoie vrai ou faux selon que le graphe est sans circuit ou non.
Implémentez et testez la fonction topological_sort() qui renvoie les sommets du graphes en ayant effectué un tri topologique.
Autres fichiers :
Plus court chemin - Bellman-Ford
Rappel de l'algorithme:
INITIALIZE-SINGLE-SOURCE(G, s) for each vertex vV(G) do d[v]
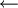
π[v]
NIL d[s]
0 RELAX(u, v, w) if d[v] > d[u] + w(u, v) then d[v] = d[u] + w(u,v) π[v]
u BELLMAN-FORD(G, s, w) INITIALIZE-SINGLE-SOURCE(G, s) for i
1 to |V(G)| - 1 do for each edge (u,v)
E(G) do RELAX(u, v, w)
Ajoutez la fonction à votre librairie et testez la sur le graphe Media:M1BBS Graphe Bellman-Ford.tab à partir du sommet A.
Ecrire un script qui prend en paramètre le fichier au format TAB contenant le graphe + un sommet source + un sommet destination et qui affiche un plus court chemin s'il existe. Le script, que l'on appelera best_path.py, pourrait commencer de la manière suivante :
#!/bin/env python from pprint import pprint import sys import numpy as np import Graph as pyg # paramètres de la ligne de commande (graph_file, source, destination) = sys.argv[1:4] print(f'file: {graph_file}') print(f'source node: {source}') print(f'destination node: {destination}') # chargement du graphe g = pyg.load_TAB(graph_file, directed=False, column_separator=' ')
Complétez le script ci-dessus pour qu'il affiche le nombre de sommets et d'arêtes dans le graphe puis utilise Bellman-Ford pour calculer les plus courts chemins à partir du sommet source fourni en ligne de commande. Vous pourrez tester votre script sur le fichier téléchargé et filtré depuis STRINGdb. Afin d'afficher le "meilleur" chemin, il faudra transformer les poids des arêtes (à interpréter comme la probabilité multipliée par 1000 qu'il y ait une association entre 2 protéines). Le meilleur chemin étant celui qui a la plus forte probabilité (produit des probabilités de chaque arête), et Bellman-Ford cherchant à minimiser le poids du meilleur chemin, (somme des poids de chaque arête), vous pourrez attribuer le poids d'une arête comme étant : weight = -log10(combined_score/1000)
Pour les protéines rnE (ribonuclease E ou b1084) et dnaJ (b0015 co-chaperon de dnaK), vous devriez obtenir la sortie suivante :
./best.path.py 511145.protein.links.filtered.700.txt 511145.b0015 511145.b1084
file: 511145.protein.links.filtered.700.txt source node: 511145.b0015 destination node: 511145.b1084 number of nodes: 2840 number of edges: 19024 best path: ['511145.b0015', '511145.b0014', '511145.b2231', '511145.b3699', '511145.b3701', '511145.b3702', '511145.b4052', '511145.b4361', '511145.b4362', '511145.b4201', '511145.b4202', '511145.b4203', '511145.b4173', '511145.b4172', '511145.b0143', '511145.b3164', '511145.b1084']
Utilisation de git et prise en main pour la Gene Ontology
Informations à suivre sur gitlab : https://gitlab.com/rbarriot/guides/-/tree/master/git#d%C3%A9marrage-cloner-un-projet
Plus courts chemins - Floyd-Warshall
Pour l'agorithme suivant,
- D[x,y] est la distance du plus court chemin entre les sommets x et y
- N[x,y] est le successeur de x dans le plus court chemin allant de x à y
- W[x,y] est la valuation de l'arc (x,y)
Algorithme :
initialiser D = W, et N à partir des arcs/arêtes du graphe
pour k de 1 à n
pour i de 1 à n
pour j de 1 à n
si D[i,k] + D[k,j] < D[i,j] alors
D[i,j] = D[i,k] + D[k,j]
N[i,j] = N[i,k]
Récupération du plus court chemin à partir de la matrice N :
plusCourtChemin(D,N, i,j)
si D[i,j] est infinie alors
il n'y a pas de chemin entre i et j
chemin = initialiserChemin(i)
k = N[i,j]
tant que k est défini faire
ajouter(chemin, k)
k = N[k,j]
ajouter(chemin, j)
Implémentez les fonctions FloydWarshall(W) et FloydWarshallPath(source, destination) dans votre librairie. Pour cela, vous êtes forcement incité(e) à ajouter une fonction adjacency_matrix qui renvoie le graphe source forme de matrice d'adjacence.
Aide : Création d'une matrice de 10 lignes et 20 colonnes initialisées avec des valeurs infinies avec numpy
import numpy as np matrix = np.full( (10, 20), np.inf )
Testez ces fonctions sur le graphe Media:M1BBS Graphe Floyd-Warshall.tab et affichez les plus courts chemins de A à C et de A à B (avec leur longueur).
Quel est le diamètre du graphe ? Affichez le chemin correspondant.
Dijkstra
Dijkstra(G,w,s) INITIALIZE-SINGLE-SOURCE(G, s) QV[G] while Q
do u
EXTRACT-MIN(Q) for each v
Adj[u] do RELAX(u,v,w)
Pour une plus grande efficacité, il faudra utiliser une file avec priorités (priority queue) pour la ligne avec EXTRACT-MIN. La file contiendra donc les sommets à parcourir, du plus proche au plus éloigné.
Le langage python propose le module heapq permettant de gérer ce type de file. Néanmoins, une fois inséré dans la file, il n'est plus possible de changer la priorité d'un élément. Pour simplifier pour cette fois, on pourra insérer de nouveau le sommet dans la file (mais avec une distance plus faible) plutôt que de modifier sa priorité. Pour ne pas traiter un sommet plusieurs fois, il faudra donc s'assurer que le sommet extrait de la file avec EXTRACT-MIN est bien réellement à traiter.
Algorithmes adaptés pour python :
RELAX(u, v, w)
if d[v] > d[u] + w(u, v)
then d[v] = d[u] + w(u,v)
π[v] 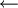 u
return True
return False
u
return True
return False
Remarque : RELAX renvoie maintenant True ou False selon que l'arc a été relaxé (la distance du sommet v à s a diminué) ou non.
Dijkstra(G,w,s) INITIALIZE-SINGLE-SOURCE(G, s) SQ
V[G] while Q
do u
EXTRACT-MIN(Q) if u
S then S
S
u for each v
Adj[u] do if RELAX(u,v,w) then Q
Q
(u, d[u])
Aide sur heapq : pour insérer un sommet avec une priorité dans la file, récupérer le plus proche, ... :
import heapq pq = [] # initialize empty priority queue # insertion u = 'A' distA = 10 heapq.push(pq, [ distA, u ] ) # get first element u = heapq.heappop()[1] # get first element together with its priority (d, u) = heapq.heappop()
Graphe vu en cours : Media:M1BBS Graphe Dijkstra.tab
Pour aller plus loin
Idées d'algorithme à ajouter à la librairie pour s'exercer :
- Exercice du cours sur la durée minimale d'un projet ainsi que le ou les chemins critiques et les tâches critiques.
Idées de d'applications :
- Arbitrage à partir d'une matrice de taux de change
Annexe
Sortie typique
$ ./Graph.py
Graph lib tests
#########################
### create_graph and load_SIF
{'directed': True,
'edges': {'ceinture': {'veste': {'type': 'avant'}},
'chaussettes': {'chaussures': {'type': 'avant'}},
'chaussures': {},
'chemise': {'ceinture': {'type': 'avant'},
'cravate': {'type': 'avant'}},
'cravate': {'veste': {'type': 'avant'}},
'pantalon': {'ceinture': {'type': 'avant'},
'chaussures': {'type': 'avant'}},
'sous-vetements': {'chaussures': {'type': 'avant'},
'pantalon': {'type': 'avant'}},
'veste': {}},
'in_edges': {'ceinture': {'chemise': {'type': 'avant'},
'pantalon': {'type': 'avant'}},
'chaussettes': {},
'chaussures': {'chaussettes': {'type': 'avant'},
'pantalon': {'type': 'avant'},
'sous-vetements': {'type': 'avant'}},
'chemise': {},
'cravate': {'chemise': {'type': 'avant'}},
'pantalon': {'sous-vetements': {'type': 'avant'}},
'sous-vetements': {},
'veste': {'ceinture': {'type': 'avant'},
'cravate': {'type': 'avant'}}},
'nb_edges': 9,
'nodes': {'ceinture': {},
'chaussettes': {},
'chaussures': {},
'chemise': {},
'cravate': {},
'pantalon': {},
'sous-vetements': {},
'veste': {}},
'weight_attribute': None,
'weighted': False}
#### BFS ####
nb_edges: 9
in_edges: {'chaussettes': {}, 'chaussures': {'chaussettes': {'type': 'avant'}, 'pantalon': {'type': 'avant'}, 'sous-vetements': {'type': 'avant'}}, 'pantalon': {'sous-vetements': {'type': 'avant'}}, 'chemise': {}, 'cravate': {'chemise': {'type': 'avant'}}, 'ceinture': {'chemise': {'type': 'avant'}, 'pantalon': {'type': 'avant'}}, 'veste': {'cravate': {'type': 'avant'}, 'ceinture': {'type': 'avant'}}, 'sous-vetements': {}}
directed: True
weighted: False
weight_attribute: None
Nodes:
chaussettes :
chaussures :
pantalon :
chemise :
cravate :
ceinture :
veste :
sous-vetements :
Edges
chaussettes -> chaussures
type : avant
pantalon -> chaussures
type : avant
pantalon -> ceinture
type : avant
chemise -> cravate
type : avant
chemise -> ceinture
type : avant
cravate -> veste
type : avant
ceinture -> veste
type : avant
sous-vetements -> chaussures
type : avant
sous-vetements -> pantalon
type : avant
nb_edges: 9
in_edges: {'chaussettes': {}, 'chaussures': {'chaussettes': {'type': 'avant'}, 'pantalon': {'type': 'avant'}, 'sous-vetements': {'type': 'avant'}}, 'pantalon': {'sous-vetements': {'type': 'avant'}}, 'chemise': {}, 'cravate': {'chemise': {'type': 'avant'}}, 'ceinture': {'chemise': {'type': 'avant'}, 'pantalon': {'type': 'avant'}}, 'veste': {'cravate': {'type': 'avant'}, 'ceinture': {'type': 'avant'}}, 'sous-vetements': {}}
directed: True
weighted: False
weight_attribute: None
Nodes:
chaussettes :
chaussures :
pantalon :
chemise :
cravate :
ceinture :
veste :
sous-vetements :
Edges
chaussettes -> chaussures
type : avant
pantalon -> chaussures
type : avant
pantalon -> ceinture
type : avant
chemise -> cravate
type : avant
chemise -> ceinture
type : avant
cravate -> veste
type : avant
ceinture -> veste
type : avant
sous-vetements -> chaussures
type : avant
sous-vetements -> pantalon
type : avant
### BFS distances
[('sous-vetements', 0), ('chaussures', 1), ('pantalon', 1), ('ceinture', 2), ('veste', 3), ('chaussettes', inf), ('chemise', inf), ('cravate', inf)]
#########################
#### DFS ####
{'directed': True,
'edges': {'ceinture': {'veste': {'type': 'avant'}},
'chaussettes': {'chaussures': {'type': 'avant'}},
'chaussures': {},
'chemise': {'ceinture': {'type': 'avant'},
'cravate': {'type': 'avant'}},
'cravate': {'veste': {'type': 'avant'}},
'pantalon': {'ceinture': {'type': 'avant'},
'chaussures': {'type': 'avant'}},
'sous-vetements': {'chaussures': {'type': 'avant'},
'pantalon': {'type': 'avant'}},
'veste': {}},
'in_edges': {'ceinture': {'chemise': {'type': 'avant'},
'pantalon': {'type': 'avant'}},
'chaussettes': {},
'chaussures': {'chaussettes': {'type': 'avant'},
'pantalon': {'type': 'avant'},
'sous-vetements': {'type': 'avant'}},
'chemise': {},
'cravate': {'chemise': {'type': 'avant'}},
'pantalon': {'sous-vetements': {'type': 'avant'}},
'sous-vetements': {},
'veste': {'ceinture': {'type': 'avant'},
'cravate': {'type': 'avant'}}},
'nb_edges': 9,
'nodes': {'ceinture': {},
'chaussettes': {},
'chaussures': {},
'chemise': {},
'cravate': {},
'pantalon': {},
'sous-vetements': {},
'veste': {}},
'weight_attribute': None,
'weighted': False}
{'directed': True,
'edges': {'ceinture': {'veste': {'type': 'avant'}},
'chaussettes': {'chaussures': {'type': 'avant'}},
'chaussures': {},
'chemise': {'ceinture': {'type': 'avant'},
'cravate': {'type': 'avant'}},
'cravate': {'veste': {'type': 'avant'}},
'pantalon': {'ceinture': {'type': 'avant'},
'chaussures': {'type': 'avant'}},
'sous-vetements': {'chaussures': {'type': 'avant'},
'pantalon': {'type': 'avant'}},
'veste': {}},
'in_edges': {'ceinture': {'chemise': {'type': 'avant'},
'pantalon': {'type': 'avant'}},
'chaussettes': {},
'chaussures': {'chaussettes': {'type': 'avant'},
'pantalon': {'type': 'avant'},
'sous-vetements': {'type': 'avant'}},
'chemise': {},
'cravate': {'chemise': {'type': 'avant'}},
'pantalon': {'sous-vetements': {'type': 'avant'}},
'sous-vetements': {},
'veste': {'ceinture': {'type': 'avant'},
'cravate': {'type': 'avant'}}},
'nb_edges': 9,
'nodes': {'ceinture': {},
'chaussettes': {},
'chaussures': {},
'chemise': {},
'cravate': {},
'pantalon': {},
'sous-vetements': {},
'veste': {}},
'weight_attribute': None,
'weighted': False}
### Is it acyclic? True
### Topological sort
sous-vetements
chemise
cravate
pantalon
ceinture
veste
chaussettes
chaussures
### Use is_acyclic on a graph with a cycle
nb_edges: 8
in_edges: {'u': {}, 'v': {'u': {'type': 'avant'}, 'x': {'type': 'avant'}}, 'x': {'u': {'type': 'avant'}, 'y': {'type': 'avant'}}, 'y': {'v': {'type': 'avant'}, 'w': {'type': 'avant'}}, 'w': {}, 'z': {'w': {'type': 'avant'}, 'z': {'type': 'avant'}}}
directed: True
weighted: False
weight_attribute: None
Nodes:
u :
v :
x :
y :
w :
z :
Edges
u -> v
type : avant
u -> x
type : avant
v -> y
type : avant
x -> v
type : avant
y -> x
type : avant
w -> y
type : avant
w -> z
type : avant
z -> z
type : avant
Is g2 acyclic? False
### nodes reachable from String_coexpr WBBJ using dfs_visit
RFBC
RFBX
RFBD
WBBJ
WBBH
WBBK
WBBI
#### Bellman-Ford ####
{'directed': True,
'edges': {'A': {'B': {'weight': '6'}, 'E': {'weight': '7'}},
'B': {'C': {'weight': '5'},
'D': {'weight': '-4'},
'E': {'weight': '8'}},
'C': {'B': {'weight': '-2'}},
'D': {'A': {'weight': '2'}, 'C': {'weight': '7'}},
'E': {'C': {'weight': '-3'}, 'D': {'weight': '9'}}},
'in_edges': {'A': {'D': {'weight': '2'}},
'B': {'A': {'weight': '6'}, 'C': {'weight': '-2'}},
'C': {'B': {'weight': '5'},
'D': {'weight': '7'},
'E': {'weight': '-3'}},
'D': {'B': {'weight': '-4'}, 'E': {'weight': '9'}},
'E': {'A': {'weight': '7'}, 'B': {'weight': '8'}}},
'nodes': {'A': {}, 'B': {}, 'C': {}, 'D': {}, 'E': {}},
'weight_attribute': 'weight',
'weighted': True}
{'distance': {'A': 0, 'B': 2.0, 'C': 4.0, 'D': -2.0, 'E': 7.0},
'predecessor': {'A': None, 'B': 'C', 'C': 'E', 'D': 'B', 'E': 'A'}}
#### Floyd-Warshall ####
{'directed': True,
'edges': {'A': {'B': {'weight': '3'},
'C': {'weight': '8'},
'E': {'weight': '-4'}},
'B': {'D': {'weight': '1'}, 'E': {'weight': '7'}},
'C': {'B': {'weight': '4'}},
'D': {'A': {'weight': '2'}, 'C': {'weight': '-5'}},
'E': {'D': {'weight': '6'}}},
'in_edges': {'A': {'D': {'weight': '2'}},
'B': {'A': {'weight': '3'}, 'C': {'weight': '4'}},
'C': {'A': {'weight': '8'}, 'D': {'weight': '-5'}},
'D': {'B': {'weight': '1'}, 'E': {'weight': '6'}},
'E': {'A': {'weight': '-4'}, 'B': {'weight': '7'}}},
'nodes': {'A': {}, 'B': {}, 'C': {}, 'D': {}, 'E': {}},
'weight_attribute': 'weight',
'weighted': True}
D:
array([[ 0., 1., -3., 2., -4.],
[ 3., 0., -4., 1., -1.],
[ 7., 4., 0., 5., 3.],
[ 2., -1., -5., 0., -2.],
[ 8., 5., 1., 6., 0.]])
N:
array([[0, 4, 4, 4, 4],
[3, 1, 3, 3, 3],
[1, 1, 2, 1, 1],
[0, 2, 2, 3, 0],
[3, 3, 3, 3, 4]])
### Shortest path from A to B
path: ['A', 'E', 'D', 'C', 'B'], length: 1.0
### from A to C
path: ['A', 'E', 'D', 'C'], length: -3.0
### from E to C
path: ['E', 'D', 'C'], length: 1.0
### from E to A
path: ['A', 'E', 'D', 'C'], length: -3.0
### graph diameter: 8.0
#### Dijkstra ####
{'directed': True,
'edges': {'A': {'B': {'weight': '10'}, 'E': {'weight': '5'}},
'B': {'C': {'weight': '1'}, 'E': {'weight': '2'}},
'C': {'D': {'weight': '4'}},
'D': {'A': {'weight': '7'}, 'C': {'weight': '6'}},
'E': {'B': {'weight': '3'},
'C': {'weight': '9'},
'D': {'weight': '2'}}},
'in_edges': {'A': {'D': {'weight': '7'}},
'B': {'A': {'weight': '10'}, 'E': {'weight': '3'}},
'C': {'B': {'weight': '1'},
'D': {'weight': '6'},
'E': {'weight': '9'}},
'D': {'C': {'weight': '4'}, 'E': {'weight': '2'}},
'E': {'A': {'weight': '5'}, 'B': {'weight': '2'}}},
'nodes': {'A': {}, 'B': {}, 'C': {}, 'D': {}, 'E': {}},
'weight_attribute': 'weight',
'weighted': True}
{'distance': {'A': 0, 'B': 8.0, 'C': 9.0, 'D': 7.0, 'E': 5.0},
'predecessor': {'A': None, 'B': 'E', 'C': 'B', 'D': 'E', 'E': 'A'}}
#### Johnson ####
in_edges: {'A': {'D': {'weight': '2'}}, 'B': {'A': {'weight': '3'}, 'C': {'weight': '4'}}, 'C': {'A': {'weight': '8'}, 'D': {'weight': '-5'}}, 'E': {'A': {'weight': '-4'}, 'B': {'weight': '7'}}, 'D': {'B': {'weight': '1'}, 'E': {'weight': '6'}}}
directed: True
weighted: True
weight_attribute: weight
Nodes:
A :
B :
C :
E :
D :
Edges
A -> B
weight : 3
A -> C
weight : 8
A -> E
weight : -4
B -> D
weight : 1
B -> E
weight : 7
C -> B
weight : 4
E -> D
weight : 6
D -> A
weight : 2
D -> C
weight : -5
after Johnson
in_edges: {'A': {'D': {'weight': 2.0}}, 'B': {'A': {'weight': 3.0}, 'C': {'weight': 4.0}}, 'C': {'A': {'weight': 8.0}, 'D': {'weight': -5.0}}, 'E': {'A': {'weight': -4.0}, 'B': {'weight': 7.0}}, 'D': {'B': {'weight': 1.0}, 'E': {'weight': 6.0}}}
directed: True
weighted: True
weight_attribute: weight
ids: ['A', 'B', 'C', 'D', 'E']
nb_edges: 9
Nodes:
A :
B :
C :
E :
D :
Edges
A -> B
weight : 3.0
A -> C
weight : 8.0
A -> E
weight : -4.0
B -> D
weight : 1.0
B -> E
weight : 7.0
C -> B
weight : 4.0
E -> D
weight : 6.0
D -> A
weight : 2.0
D -> C
weight : -5.0
array([[ 0., 1., -3., 2., -4.],
[ 3., 0., -4., 1., -1.],
[ 7., 4., 0., 5., 3.],
[ 2., -1., -5., 0., -2.],
[ 8., 5., 1., 6., 0.]])
array([[0, 4, 4, 4, 4],
[3, 1, 3, 3, 3],
[1, 1, 2, 1, 1],
[0, 2, 2, 3, 0],
[3, 3, 3, 3, 4]])
### Shortest path from A to B
path: ['A', 'E', 'D', 'C', 'B'], length: 1.0
### graph diameter: 8.0