M1 Traitement de Donnees Biologiques - Transcriptome - Oryza sativa
From silico.biotoul.fr
Installation des librairies spécifiques à l'analyse de transcriptome
A NE FAIRE QUE S'IL MANQUE CES LIBRAIRIES
Via la console de RStudio, on installe les packages suivants (disponibles sur Bioconductor):
Pour R version ≥ 3.5
install.packages("BiocManager") BiocManager::install(c("affy", "limma", "AnnotationDbi", "ricecdf", "made4"))
Pour R version < 3.5
source('https://bioconductor.org/biocLite.R') biocLite('affy') biocLite('limma') biocLite('AnnotationDbi') biocLite("made4")
Préparation de l'environnement
Dans ce TP, nous allons analyser les données de transciptome obtenues sur Oryza sativa par microarray. Le déroulement des analyses suit les travaux de Fujita et al. publiés en 2010 (pmid:21062870). Il vous est conseillé de prendre connaissance de l'article, tout du moins son résumé avant de commencer le TP.
Créez tout d'abord un répertoire de travail sur le bureau (par exemple TDB-TP5) et commencez par télécharger le fichier source que vous allez utiliser et compléter pour générer le compte rendu de TP : M1.TDB.TP_Transcriptome.Rmd (click droit de la souris -- enregistrer la cible sous...). Ouvrez le logiciel RStudio et chargez ce fichier puis lancez sa compilation pour voir le compte rendu. Pour cela cliquez sur le bouton Knit HTML ou bien utilisez la combinaison de touches Ctrl + shift + K.
Récupération des données
Les données relatives à l'analyse ont été mises à disposition sur la banque GEO et sont accessibles avec l'identifiant GSE14304.
Il s'agit de 98 hybridations réalisées avec un microarray de la société Affymetrix ayant l'identifiant GPL2025 comportant 57 381 spots correspondant à 51 279 transcrits d'Oryza sativa japonica et indica.
La quantité de données étant un peu volumineuse pour ce TP, nous allons travailler sur certaines conditions en particulier ; celles spécifiées dans la publication : les gènes différentiellement exprimés entre les stades P1 (Anther, uni-nuclear pollen) et P3 (Anther, tri-cellular pollen).
Chargement et exploration des données
A partir de là, on peut travailler en mode RMarkdown sous RStudio. Cependant, la compilation étant longue, il est conseillé de travailler avec la console, et de tester de temps en temps la compilation.
Librairies R/BioConductor nécessaires au TP :
library(affy) library(limma)
Chargement des données de microarray après analyse d'image :
P1P3.files = c('GSM351444.CEL.gz', 'GSM351445.CEL.gz', 'GSM351446.CEL.gz', 'GSM351450.CEL.gz', 'GSM351451.CEL.gz', 'GSM351452.CEL.gz') P1P3.raw=ReadAffy(filenames=P1P3.files)
Visualisation et exploration du contenu
P1P3.rawVisualisation des distributions des intensités de fluorescence par hybridation sous forme de boîtes à moustaches :
boxplot(P1P3.raw)
Y aurait-il besoin d'une normalisation ?
La commande hist, comme son nom ne l'indique pas, permet de tracer des courbes de densités des distributions des intensités sur la puce.
hist(P1P3.raw)
Que pensez-vous des intensités de fluorescences sur les hybridations ?
Prétraitement des données
Nous allons utiliser les mêmes paramètres que dans la publication des auteurs afin d'essayer d'obtenir les même résultats : reportez-vous à la section Materials & Methods dans la partie Microarray data extraction, processing and cluster analysis.
Prétraitement : correction du bruit de fond sans normalisation avec les paramètres décrits dans la publi :

Il vous faut donc utiliser avec les paramètres repérés dans le texte ci-dessus la commande expresso (remplacer les ...) :
P1P3.bgcorr = expresso(P1P3.raw, bgcorrect.method='...', normalize=..., pmcorrect.method='...', summary.method='...')
Le paramètre pmcorrect est spécifique à Affymetrix : il ne tient compte que des oligos (probesets) qui ont un perfect match.
Pour mettre à l'échelle au 75ème percentile (comme indiqué par les auteurs), la fonction apply permettra de le faire sur chacune des hybridations (la fonction exprs extrait les valeurs d'expression de chaque probeset) :
P1P3.scaled = exprs(P1P3.bgcorr) dim(P1P3.scaled) P1P3.scaled[,1] = P1P3.scaled[,1]/ quantile(P1P3.scaled[,1], probs=c(0.75)) P1P3.scaled[,2] = P1P3.scaled[,2]/ quantile(P1P3.scaled[,2], probs=c(0.75)) P1P3.scaled[,3] = P1P3.scaled[,3]/ quantile(P1P3.scaled[,3], probs=c(0.75)) P1P3.scaled[,4] = P1P3.scaled[,4]/ quantile(P1P3.scaled[,4], probs=c(0.75)) P1P3.scaled[,5] = P1P3.scaled[,5]/ quantile(P1P3.scaled[,5], probs=c(0.75)) P1P3.scaled[,6] = P1P3.scaled[,6]/ quantile(P1P3.scaled[,6], probs=c(0.75))
Plutôt que de devoir écrire la même commande pour chacune des colonnes de P1P3.scaled, il est possible d'utiliser la fonction apply :
P1P3.scaled = apply(P1P3.scaled, 2, function(x) x / quantile(x, probs=c(0.75) ) )
Visualisation du résultat du traitement :
boxplot(log2(P1P3.scaled), las=3)
On peut reproduire les courbes de densités de la manière suivantes :
plot(density(log2(P1P3.scaled)[,5]), col=5) # on commence par celle qui a la valeur maximale (ici, la 5) lines(density(log2(P1P3.scaled)[,1]),col=1) # ajout de la 1ère hybridation sur le plot précédent lines(density(log2(P1P3.scaled)[,2]),col=2) lines(density(log2(P1P3.scaled)[,3]),col=3) lines(density(log2(P1P3.scaled)[,4]),col=4) lines(density(log2(P1P3.scaled)[,6]),col=6)
Un commentaire ?
Analyse différentielle
Utilisation de la librairie limma et préparation à l'analyse différentielle : il faut indiquer quelle hybridation correspond à quelle condition :
design=matrix( c(rep(1:0,3), rep(0:1,3)), ncol=2, byrow=TRUE) colnames(design)=c('P1','P3') design
Analyse :
contrasts=makeContrasts(P1vsP3=P1-P3, levels=design) contrasts fit = lmFit(P1P3.scaled, design) # modèle linéaire: calcule la moyenne de P1 et P3 pour chaque probeset fit2=contrasts.fit(fit, contrasts) # calcul des contrastes (différence des moyennes P1 et P3) efit = eBayes(fit2) # modèle bayésien (calcule les statistiques modifiées de t, F, puis p-value)
Puis extraction des probesets ayant une p-valeur significative (seuil de 0.05 sur p-valeur ajustée par la FDR (BH pour Benjamini et Hochberg)) et une variation d’expression supérieure à 10 :
deg=topTable(efit, adjust='BH', p.value=0.05, number=10000, resort.by="logFC", lfc=log2(10)) dim(deg) head(deg) # premières lignes du tableau (remarque: logFC correspond ici à la différence des moyennes P1 et P3)
Combien de gènes obtient-on ? pouvait-on s'y attendre ? dans quoi (quel processus biologique) sont-ils impliqués ? Que font-ils ?
Est-ce qu’on a le probeset de la figure 3-B et pas ceux de C et D (car non différentiellement exprimés entre P1-P3) ?
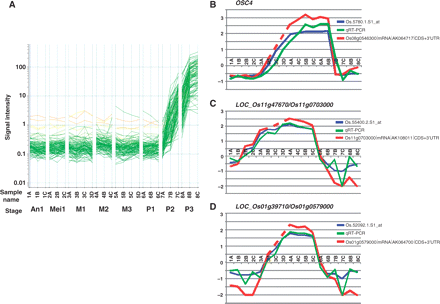
deg['Os.5780.1.S1_at',] deg['Os.55400.2.S1_at',] deg['Os.52092.1.S1_at',]
Vérification de la figure 3
Remarque : Cette partie est données à titre d'illustration.
Comme le traitement des données prend un peu de temps et de mémoire, le résultat du traitement vous est fourni ici : P1-P3.induced.profiles.txt. Ce fichier contient les profils d'expression sur 33 organes et stades de développement (un total de 98 hybridations), de 150 gènes différentiellement exprimés (avec un ratio d'expression >10) entre P1 et P3 (comme indiqué dans la légende de la figure 3).
induced.profiles=read.table('http://silico.biotoul.fr/site/images/c/c8/P1-P3.induced.profiles.txt') dim(induced.profiles)
Il s'agit ensuite d'afficher les profils en spécifiant les 26 conditions étudiées dans la figure 3 de la publication:
plot(x=1:26, y=rep(0,26), ylim=c(0, max(induced.profiles[,1:26])), pch='', las=3, xaxt='n', xlab='', ylab='') # initialisation apply(induced.profiles, 1, function(x) lines(1:26, x[1:26], col='green') ) # pour chacune des lignes/profils, ajout du profil des 26 1ères hybridations axis(1, at=1:26, labels=c('An1.1A','An1.1B','An1.1C','Mei1.2A','Mei1.2B','Mei1.2C','M1.3A','M1.3B','M1.3C','M1.3D','M2.4A','M2.4B','M2.4C','M3.5A','M3.5B','M3.5C','M3.5D','P1.6A','P1.6B','P1.6C','P2.7A','P2.7B','P2.7C','P3.8A','P3.8B','P3.8C'), las=3)
Caractérisation d'un ensemble de gènes : recherche d'annotations de la Gene Ontologie sur-représentées
Parmi les “gènes” des différentiellement exprimés identifiés précédemment, y a-t-il des annotations sur-représentées, autrement dit, ces gènes sont-ils impliqués dans des processus biologiques particuliers ?
Les identifiants des probesets peuvent être obtenus avec la commande suivante pour faciliter un copier/coller (ou bien on peut utiliser write.table pour les sauvegarder dans un fichier et l'ouvrir avec libreOffice pour effectuer le copier/coller de la colonne avec les identifiants) :
cat (rownames(deg) )
Allez sur le serveur silico.biotoul.fr afin d'effectuer cette recherche en enrichissement d'annotations de la Gene Ontology : https://silico.biotoul.fr/enrichment/
Remarque : Dans les résultats affichés, il y a un bouton permettant de pré-remplir le formulaire d'un autre site Web (REVIGO) qui analyse les annotations GO et leur p-valeur pour les visualiser de manière plus synthétique qui s'appuie sur la similarité des annotations.
Analyse de clustering
Une sélection de probesets a été effectuée pour cette partie dans laquelle, les profils d'expression sélectionnés (profiles.for.clustering.txt) vont être regroupés en clusters.
Chargement et visualisation des profils d'expression sélectionnés sur l'ensemble des hybridations (98):
profiles=read.table('http://silico.biotoul.fr/site/images/9/97/M1_TDB_Transciptome_rice_-_profiles.for.clustering.txt') dim(profiles) plot(x=1:98, y=rep(0,98), ylim=c(0, max(profiles)), pch='', las=3, xlab='', ylab='') apply(profiles, 1, function (x) lines(1:98, x, col='green') )
Afin de visualiser la similarité/dissemblance entre profils, il est possible de faire une analyse en composantes principales (ACP) sur la matrice individus (les 287 probesets) - variables (les 98 hybridations) et faire la projection sur les 2 composantes principales (les deux 1er axes ou composantes principales portant le plus de variance) :
pca = prcomp(profiles) plot(pca$x, pch=16)
Si sur cette projection, on distingue des groupes (nuages de points distincts), alors on devrait pouvoir les identifier avec du clustering. Par contre, si on ne distingue pas visuellement de groupes, c'est peut-être que la projection réalisée ne capture pas toute l'information dans les données de départ et peut-être qu'une troisième (voire 4ème, voire ...) pourrait permettre de distinguer des groupes. On se pose alors la question de la proportion d'information que l'on visualise (proportion de variance portée par les axes ) :
summary(pca)$importance[, 1:8]
Clustering hiérarchique
Chargement de la librairie pour le graphique
library(made4)
Clustering hiérarchique avec la fonction heatplot. Cette fonction effectue le clustering ascendant en fusionnant à chaque étape les 2 clusters les plus proches (ici identifiés avec le lien simple Les paramètres cols.defaults, lowcol et highcol permettent de spécifier les couleurs recommandées pour la plus large audience, notamment pour les personnes ne distinguant pas bien entre le rouge et le bleu ou le vert.
Utilisation du lien simple pour la fusion des clusters :
heatplot(profiles, method='single')
Que remarquez-vous ?
Autre méthode d'aggrégation des clusters :
heatplot(profiles, method='ward.D',scale='none')
Laquelle sélectionnerez-vous ?
Calcul de la matrice de distance entre chaque paire de gènes/probesets/profils
d=dist(profiles)
Utilisation de hclust et cutree pour sélectionner les clusters
hc = hclust(d, method='ward.D') plot(hc) rect.hclust(hc, k=3) # k=3 : on veut 3 groupes
Récupération des groupes obtenus
hc_clusters=cutree(hc, k=3) table(hc_clusters)
On peut, à présent, visualiser les profils d'expression (ici pour les 26 premières hybridations vues précédemment qui distinguent mieux les profils) :
plot(x=1:26, y=rep(0,26), ylim=c(0, max(profiles[,1:26])), pch='', las=3, xaxt='n', xlab='', ylab='') axis(1, at=1:26, labels=c('An1.1A','An1.1B','An1.1C','Mei1.2A','Mei1.2B','Mei1.2C','M1.3A','M1.3B','M1.3C','M1.3D','M2.4A','M2.4B','M2.4C','M3.5A','M3.5B','M3.5C','M3.5D','P1.6A','P1.6B','P1.6C','P2.7A','P2.7B','P2.7C','P3.8A','P3.8B','P3.8C'), las=3) hc_cluster1 = which(hc_clusters==1) foo=apply(profiles[hc_cluster1,1:26], 1, function(x) lines(1:26, x, col='#29B462')) hc_cluster2 = which(hc_clusters==2) foo=apply(profiles[hc_cluster2,1:26], 1, function(x) lines(1:26, x, col='orange')) hc_cluster3 = which(hc_clusters==3) foo=apply(profiles[hc_cluster3,1:26], 1, function(x) lines(1:26, x, col='blue'))
Observe-t-on une bonne cohésion ainsi qu'une bonne séparation des clusters ?
Visualisation sur la projection de l'ACP précédente :
plot(pca$x, col=c('#29B462','orange','blue')[hc_clusters], pch=16)
Observe-t-on une bonne cohésion ainsi qu'une bonne séparation des clusters sur cette projection ?
k-means
Nous allons utiliser maintenant la méthode k-means pour détecter les clusters au sein des profils en spécifiant le nombre de groupes à détecter.
km_clusters = kmeans(profiles, 3)$cluster table(km_clusters)
Pour comparer visuellement les clusters obtenus avec le clustering hiérarchique précédemment réalisé, en utilisant le graphique précédent et en indiquant les couleurs à utiliser correspondant aux groupes détectés :
par(mfrow=c(1,2)) plot(pca$x, pch=16, col=c('#29B462','orange','blue')[hc_clusters], main='hierarchical') plot(pca$x, pch=16, col=c('blue','#29B462','orange')[km_clusters], main='k-means')
Commentez ces résultats.
Envoyer le compte rendu à votre enseignant par mail (maxime.bonhomme@univ-tlse3.fr ou roland.barriot@univ-tlse3.fr). Le compte rendu est à envoyer avant une semaine. Envoyez les 2 fichiers (.Rmd et .html). Envoyez-vous aussi le mail en copie pour pouvoir vérifier que tout est bien passé. Mettez un titre tel que "Compte rendu TP5 TDB de -et votre Nom et Prénom-". Votre compte-rendu ne doit pas être un simple "copié-collé" des commandes. Nous attendons une mise en forme correcte (titres, sous-titres, paragraphes, ...), des commentaires (notamment sur les résultats des commandes), des essais de votre part pour améliorer par exemple la visualisation d'un graphique, ou pour rechercher des fonctions R alternatives ou complémentaires à ce qui est proposé; bref une personnalisation de votre compte-rendu !
Annexes