silico.biotoul.fr
 

InfoBio TD Matrices PAM

From silico.biotoul.fr

(Difference between revisions)
Jump to: navigation, search
m (→Calcul d'une matrice de substitution à partir d'alignements)
m (→Application aux matrices de substitution pour les alignements de séquences)
Line 31: Line 31:
* calcul des valeurs propres et des vecteurs propres : <tt>eigen(M)</tt>
* calcul des valeurs propres et des vecteurs propres : <tt>eigen(M)</tt>
-
= Application aux matrices de substitution pour les alignements de séquences =
+
= Application aux matrices de substitution pour les alignements de séquences protéiques =
-
 
+
-
== Calcul d'une matrice de substitution à partir d'alignements ==
+
cf. [[silico:enseignement/L3-Biologie/Alignement_seq_prot_2015.pdf|Alignement de deux séquences protéiques]] concernant le cours.
cf. [[silico:enseignement/L3-Biologie/Alignement_seq_prot_2015.pdf|Alignement de deux séquences protéiques]] concernant le cours.
Line 40: Line 38:
* compter le nombre de substitutions observées pour chaque acide aminé (a.a.),  
* compter le nombre de substitutions observées pour chaque acide aminé (a.a.),  
* à transformer ce nombre d'occurrence en fréquence,
* à transformer ce nombre d'occurrence en fréquence,
-
* puis à calculer la log odds matrix : la matrice contenant le coût attribué à chaque substitution (match et mismatch).
+
* ramener les fréquences de mutations telles que l'on ait 1 mutation acceptée sur 100 a.a. Cela correspond à une unité de distance évolutive (PAM1).
 +
* multiplier la matrice par elle-même pour obtenir la distance évolutive souhaitée (ici PAM120)
 +
* calculer la log odds matrix : la matrice contenant le coût attribué à chaque substitution (match et mismatch).
 +
== Fréquence de mutation d'un a.a. en un autre à partir d'alignements ==
La première étape (déjà réalisée pour vous) consiste à réaliser les alignements et à dénombrer le nombre de passage d'un acide aminé à un autre.
La première étape (déjà réalisée pour vous) consiste à réaliser les alignements et à dénombrer le nombre de passage d'un acide aminé à un autre.
Line 70: Line 71:
</source>
</source>
 +
== Fréquences des a.a. dans les séquences de départ ==
 +
 +
Nous avons donc besoin de calculer la fréquences de chaque acide aminé dans une séquence (ici, fréquences d'apparition dans nos alignements de départ). Utilisez donc la matrice <tt>CM</tt> de départ qui contient le nombre de substitutions observées pour calculer le vecteur <tt>Freq</tt> contenant la fréquence de chacun de a.a.
 +
 +
Vous devriez obtenir le vecteur suivant :
 +
<source lang="rsplus">
 +
round(Freq,2)
 +
  A    R    N    D    C    Q    E    G    H    I    L    K    M    F    P    S    T    W    Y    V
 +
0.08 0.05 0.04 0.06 0.01 0.03 0.07 0.09 0.02 0.07 0.09 0.06 0.02 0.04 0.04 0.05 0.06 0.01 0.03 0.08
 +
</source>
 +
 +
== Taux de mutations correspondant à la matrice MM ==
 +
 +
A partir des fréquences d'apparition des a.a. calculées ci-dessus et de leur probabilité de muter, calculez le nombre de mutations que l'on s'attend à avoir sur une séquence de 100 a.a. Vous devriez obtenir 43,9 mutations.
 +
 +
== Recherche de MM1 telle que le taux de mutation soit 0.01 ==
 +
 +
La matrice PAM1 correspond à 1 mutation acceptée sur 100 a.a., le taux de mutation de cette matrice doit donc être 0.01 or ce n’est pas le cas de la matrice MM.
 +
 +
Le pourcentage d’a.a. qui ne change pas est <math>x = 100 \sum_i f_i M_{ii}</math> avec <math>M_{ii}</math> la probabilité de ne pas muter ou bien encore <math>x = \sum_i f_i (1 - \lambda m_i)</math> avec <math>m_i</math> la probabilité de muter.
 +
 +
on en déduit <math>\lambda = \frac{100 - x}{100 \sum_i f_i m_i}</math> et on peut mettre à l'échelle MM afin que le pourcentage de mutations soit 1 : <math>\lambda = \frac{1}{100 \sum_i f_i m_i}</math>.
 +
 +
On a donc <math>MM1_{ij} = MM1_{ij} \times \lambda</math> si i différent j et sinon <math>MM1_{ii} \times (1 - \lambda)</math>
 +
 +
Vous devriez obtenir ceci (10 premières lignes et 10 premières colonne) :
 +
<source lang="rsplus">
 +
round(MM1*10000)[1:10,1:10]
 +
    A    R    N    D    C    Q    E    G    H    I
 +
A 9903    4    6    5  14    8    9    9    4    4
 +
R    3 9898    5    2    3  10    5    2    6    1
 +
N    3    4 9915  11    2    5    5    5    8    1
 +
D    4    3  16 9898    1    7  20    4    6    0
 +
C    2    1    1    0 9898    0    0    0    1    1
 +
Q    3    7    5    4    1 9926    9    1    6    1
 +
E    7    6    8  24    1  19 9907    3    6    1
 +
G    9    3    9    5    3    3    4 9862    3    1
 +
H    1    3    4    2    1    4    2    1 9904    0
 +
I    3    2    2    1    5    2    1    0    1 9911
 +
</source>
 +
 +
== Calcul de la matrice de substitution ==
Pour un alignement de l'acide aminé <math>AA_i</math> avec l'acide aminé <math>AA_j</math>, on utilise la formule suivante :
Pour un alignement de l'acide aminé <math>AA_i</math> avec l'acide aminé <math>AA_j</math>, on utilise la formule suivante :
Line 89: Line 132:
 +
Pour les fréquences de mutations de MM120 correspondant à 120 unités MM1, il faut multiplier 120 fois MM1 avec elle-même (produit vectoriel).
-
Nous avons donc besoin de calculer la fréquences de chaque acide aminé dans une séquence (ici, fréquences d'apparition dans nos alignements de départ). Utilisez donc la matrice <tt>CM</tt> de départ qui contient le nombre de substitutions observées pour calculer le vecteur <tt>Freq</tt> contenant la fréquence de chacun de a.a.
 
-
 
-
Vous devriez obtenir le vecteur suivant :
 
<source lang="rsplus">
<source lang="rsplus">
-
round(Freq,2)
+
round(MM120*100)
-
   A   R   N   D   C   Q   E   G   H   I   L   K   M   F   P   S   T   W   Y   V  
+
   A R N D C Q E G H I L K M F P S T W Y V
-
0.08 0.05 0.04 0.06 0.01 0.03 0.07 0.09 0.02 0.07 0.09 0.06 0.02 0.04 0.04 0.05 0.06 0.01 0.03 0.08
+
A 33  3  5  4  7  6  5  4  3  4  3  5  5  2  4 11  6  1  2  6
 +
R  2 31  4  2  2  6  3  1  4  1  1  9  2  1  1  3  3  1  1  1
 +
N  2  3 38  5  2  4  3  2  4  1  1  4  2  1  1  5  3  1  2  1
 +
D  3  2  8 32  1  5  9  2  4  1  1  4  1  1  2  5  3  1  1  1
 +
C  1  0 1  0 30  0 0 0 0 1  0 0 1  1  0 1  1  1  1  1
 +
Q  2  4  4  3  1 43  6  1  4  1  2  6  3  1  1  4  3  1  1  2
 +
E  4  4  6 11  2 11 36  2  4  2  1  7  3  1  2  6  4  1  2  2
 +
G  3  2  4  2  2  2  2 19  2  1  1  2  1  1  1  4  2  1  1  1
 +
H  1  1  2  1  1  2  1  0 32  1  1  2  1  1  1  1  1  1  3  1
 +
I  3  2  2  1  4  3  2  1  2 39  9  2 11  4  1  2  4  2  2 15
 +
L  3  2  2  1  3  4  2  1  3 12 30  3 16  7  2  3  3  3  4  8
 +
K  4 11  7  4  2 10  7  2  5  2  2 38  3  1  2  6  4  1  2  2
 +
M  1  1  1  1  1  2  1  0 1  4  4  1 42  2  1  1  2  1  1  3
 +
F  1  1  1  1  2  1  1  0 3  3  3  1  4 29  0 1  1  5  9  2
 +
P  2  1  1  1  1  2  1  1  1  1  1  1  1  0 21  2  1  0 1  1
 +
S  7  4  7  5  5  6  5  3  4  2  2  5  3  2  3 42  9  2  2  3
 +
T  4  3  5  3  5  5  4  1  3  3  2  4  4  2  2  9 35  1  2  4
 +
W  0 0 0 0 0 0  0  0  1  0  0  0  0  1  0  0  0 22  1  0
 +
Y  1  1  1  1  1  1  1  0  4  1  1  1  2  6  0  1  1  4 28  1
 +
V  5  2  2  1  7  4  2  1  2 17  7  3  9  4  2  4  6  2  2 38
</source>
</source>
-
Il n'y a plus qu'à appliquer la formule <math>S_{i,j} = 10 \times log_{10}\frac{M_{i,j}}{F_i}</math>.
+
Ensuite, il n'y a plus qu'à appliquer la formule <math>S_{i,j} = 10 \times log_{10}\frac{M_{i,j}}{F_i}</math>.
Vous devriez obtenir la matrice de substitution suivante :
Vous devriez obtenir la matrice de substitution suivante :
<source lang="rsplus">
<source lang="rsplus">
-
round(S[1:10,1:10],1)
+
round(S120)
-
    A   R   N     D     C   Q     E     G   H     I
+
   A  R N D C Q E   G H   I   L  K  M  F  P  S  T  W  Y  V
-
A  8.1 -5.3 -4.3  -4.5 -0.2 -3.0 -2.3  -2.1 -6.2  -6.0
+
A  6 -4 -3 -3 -1 -2 -2 -4 -4 -4  -4 -3 -3  -6  -3 1 -1  -8  -6 -2
-
R -5.3 10.4 -2.7  -6.0 -4.9 0.5 -3.0 -6.4 -1.7  -8.4
+
R -4  8 -2 -4 -4  1 -2  -6 -2  -6 -6  2 -3 -7  -6 -2 -3  -7  -6  -6
-
N -4.1 -2.5 11.2   2.1  -4.3 -1.1 -1.6 -1.6 0.9 -8.0
+
N -2 -1 10  2 -3  0 0  -3 1  -5 -6 0 -4 -6  -5  1 0  -7  -3  -5
-
D -4.6 -6.0  1.8  9.9 -9.3 -1.8  2.9 -4.5 -2.2 -13.2
+
D -3 -4 1 7 -6  0  2 -5 -2 -8  -8 -2 -6  -9  -5 -1 -3 -9  -7  -7
-
C -0.3 -4.9 -4.6  -9.4  16.5 -8.4 -11.4  -6.8 -6.2 -4.4
+
C -1 -4 -3 -6 14 -5 -6 -7 -5  -3  -4 -5 -3  -3  -7  0 -1 -3  -3 -1
-
Q -2.6 0.9 -1.0  -1.3 -8.0 11.2  2.2 -6.1  0.5  -7.7
+
Q -1  1  1 0 -4 11  2 -5  1  -4  -3  2  0 -5  -3  1 -1  -5  -3  -3
-
E -2.2 -2.8 -1.7   3.0 -11.2 1.9   8.9 -5.6 -3.2 -10.4
+
E -2 -2  0  2 -6 2  7  -5 -2  -6 -7  0 -4 -8  -4 -1 -2  -8 -6  -5
-
G -2.7 -6.9 -2.4 -5.0 -7.3 -7.1 -6.3   9.3 -7.7 -14.9
+
G -4 -7 -3 -6 -7 -6 -6   3 -7 -11 -11 -6 -9 -12 -9 -4 -7 -11 -11 -10
-
H -6.2 -1.6 0.8 -2.2  -6.1  0.2  -3.3  -7.1 14.2  -9.8
+
H -4 -1 1 -2 -5  1 -2  -7 12  -6 -5 -1 -3  -2 -4 -2 -3 -2  1  -5
-
I -5.9 -8.2 -8.1 -13.0 -4.2 -7.9 -10.3 -14.1 -9.6  8.8
+
I -4 -6 -5 -8 -2 -4 -6 -10 -6  8  1 -5  2 -2  -8 -4 -2 -5 -4  4
-
 
+
L -5 -6 -6 -8 -4 -4 -7 -11 -5  1  5 -5  3  -1 -8 -5 -4  -6  -4   0
 +
K -2 3 0 -2 -5  2  0  -5 -1  -5  -5  8 -3 -7  -4 -1 -2 -8  -5  -5
 +
M -2 -3 -4 -6 -2 0 -4  -8 -2  2   3 -2 13   1 -6 -2 -1  -4 -2   1
 +
F -6 -7 -6 -9 -3 -6 -8 -11 -2  -2 -1 -7 0  9 -9 -6 -6  1  3 -3
 +
P -3 -6 -5 -6 -8 -4 -5  -9 -5  -8  -8 -5 -7 -10  7 -3 -5 -11  -9 -7
 +
S  1 -2 1 -1  0  0 -1  -3 -2 -4  -4  0 -2  -5  -2  9  2  -5  -5  -3
 +
T -1 -3 0 -3 -1 -1 -2  -6 -3  -2  -4 -2 -1 -5  -5  2 8 -8 -5 -1
 +
W -9 -7 -7 -9 -4 -6 -9 -11 -3  -6  -6 -8 -5  0 -11 -6 -8 14  1 -6
 +
Y -6 -6 -4 -7 -4 -4 -6 -11  1  -5 -4 -6 -3  3  -9 -5 -6  1  10  -5
 +
V -2 -6 -5 -7 -1 -3 -5  -9 -5  3   0 -5  1 -3  -6 -3 -1  -6  -5   7
</source>
</source>

Revision as of 16:06, 5 March 2015

Contents

Manipulation de matrices avec R 

A = matrix( c(11, 12, 13, 21, 22, 23, 31, 32, 33), ncol=3, byrow=TRUE )

Cas de la matrice unité d'ordre n (notée In), exemple avec n = 3 : 

I3 = diag(3)

Cas des vecteurs colonne ou ligne : 

V = c(1, 0, 5)
class(V)
# obtention de la matrice vecteur colonne :
as.matrix(V)
# pour obtenir la matrice vecteur ligne, on fait la transposée du résultat pécédent :
t( as.matrix(V) )
  • addition +, soustraction -, multiplication par un nombre *,
  • produit matriciel :
    • entre 2 matrices A et I3 : A %*% I3,
    • entre une matrice A et un vecteur v : A %*% v
  • transposition : t(M)
  • trace : sum( diag(M) )
  • déterminant : det(M)
  • inversion d'une matrice : solve(M)
  • calcul des valeurs propres et des vecteurs propres : eigen(M)

Application aux matrices de substitution pour les alignements de séquences protéiques

cf. Alignement de deux séquences protéiques concernant le cours.

Nous allons construire une matrice de type Dayhoff (PAM) pour l'alignement de séquences protéiques, ceci à partir d'alignements de séquences. La méthode en quelques mots consiste à

  • compter le nombre de substitutions observées pour chaque acide aminé (a.a.),
  • à transformer ce nombre d'occurrence en fréquence,
  • ramener les fréquences de mutations telles que l'on ait 1 mutation acceptée sur 100 a.a. Cela correspond à une unité de distance évolutive (PAM1).
  • multiplier la matrice par elle-même pour obtenir la distance évolutive souhaitée (ici PAM120)
  • calculer la log odds matrix : la matrice contenant le coût attribué à chaque substitution (match et mismatch).

Fréquence de mutation d'un a.a. en un autre à partir d'alignements

La première étape (déjà réalisée pour vous) consiste à réaliser les alignements et à dénombrer le nombre de passage d'un acide aminé à un autre.

Fichier contenant, le nombre de substitutions observées entre chaque paire d'acides aminés dans un lot de séquences préalablement alignées File:Count matrix.txt. 

CM=read.table("count_matrix.txt", sep="\t", header=TRUE, row.names=1)


Après avoir chargé cette matrice dans R, transformez-la en une matrice MM (mutation matrix) qui contient des fréquences (aidez-vous des fonctions apply et sum). Ces fréquences sont interprétées comme des probabilités de passer d'un acide aminé en un autre.

Vous devriez obtenir ceci (10 premières lignes et 10 premières colonne) : 

round(MM[1:10,1:10],2)
     A    R    N    D    C    Q    E    G    H    I
A 0.54 0.03 0.03 0.03 0.08 0.04 0.05 0.05 0.02 0.02
R 0.02 0.57 0.03 0.01 0.02 0.06 0.03 0.01 0.04 0.01
N 0.01 0.02 0.48 0.06 0.01 0.03 0.03 0.03 0.05 0.01
D 0.02 0.01 0.09 0.57 0.01 0.04 0.11 0.02 0.03 0.00
C 0.01 0.00 0.00 0.00 0.57 0.00 0.00 0.00 0.00 0.00
Q 0.02 0.04 0.03 0.02 0.01 0.42 0.05 0.01 0.04 0.01
E 0.04 0.04 0.05 0.13 0.01 0.11 0.52 0.02 0.03 0.01
G 0.05 0.02 0.05 0.03 0.02 0.02 0.02 0.77 0.02 0.00
H 0.00 0.01 0.02 0.01 0.01 0.02 0.01 0.00 0.54 0.00
I 0.02 0.01 0.01 0.00 0.03 0.01 0.01 0.00 0.01 0.50

Fréquences des a.a. dans les séquences de départ

Nous avons donc besoin de calculer la fréquences de chaque acide aminé dans une séquence (ici, fréquences d'apparition dans nos alignements de départ). Utilisez donc la matrice CM de départ qui contient le nombre de substitutions observées pour calculer le vecteur Freq contenant la fréquence de chacun de a.a.

Vous devriez obtenir le vecteur suivant : 

round(Freq,2)
   A    R    N    D    C    Q    E    G    H    I    L    K    M    F    P    S    T    W    Y    V 
0.08 0.05 0.04 0.06 0.01 0.03 0.07 0.09 0.02 0.07 0.09 0.06 0.02 0.04 0.04 0.05 0.06 0.01 0.03 0.08

Taux de mutations correspondant à la matrice MM

A partir des fréquences d'apparition des a.a. calculées ci-dessus et de leur probabilité de muter, calculez le nombre de mutations que l'on s'attend à avoir sur une séquence de 100 a.a. Vous devriez obtenir 43,9 mutations.

Recherche de MM1 telle que le taux de mutation soit 0.01

La matrice PAM1 correspond à 1 mutation acceptée sur 100 a.a., le taux de mutation de cette matrice doit donc être 0.01 or ce n’est pas le cas de la matrice MM.

Le pourcentage d’a.a. qui ne change pas est

x = 100∑fiMii
i

avec Mii la probabilité de ne pas muter ou bien encore

x = ∑fi(1 − λmi)
i

avec mi la probabilité de muter.

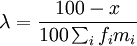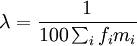on en déduit \lambda = \frac{100 - x}{100 \sum_i f_i m_i} et on peut mettre à l'échelle MM afin que le pourcentage de mutations soit 1 : \lambda = \frac{1}{100 \sum_i f_i m_i}.

On a donc 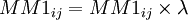MM1_{ij} = MM1_{ij} \times \lambda si i différent j et sinon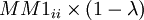 MM1_{ii} \times (1 - \lambda)

Vous devriez obtenir ceci (10 premières lignes et 10 premières colonne) : 

round(MM1*10000)[1:10,1:10]
     A    R    N    D    C    Q    E    G    H    I
A 9903    4    6    5   14    8    9    9    4    4
R    3 9898    5    2    3   10    5    2    6    1
N    3    4 9915   11    2    5    5    5    8    1
D    4    3   16 9898    1    7   20    4    6    0
C    2    1    1    0 9898    0    0    0    1    1
Q    3    7    5    4    1 9926    9    1    6    1
E    7    6    8   24    1   19 9907    3    6    1
G    9    3    9    5    3    3    4 9862    3    1
H    1    3    4    2    1    4    2    1 9904    0
I    3    2    2    1    5    2    1    0    1 9911

Calcul de la matrice de substitution

Pour un alignement de l'acide aminé AAi avec l'acide aminé AAj, on utilise la formule suivante :

\frac{P(\mathrm{alignement. AA_i. avec. AA_j. est. du. a. l'evolution})}{P(\mathrm{alignement. AA_i. avec. AA_j. est. du. au. hasard})} = \frac{F_i.M_{j,i}}{F_i.F_j} = \frac{F_j.M_{i,j}}{F_i.F_j}

avec M la matrice MM précédemment calculée (mutation matrix) et F la fréquence de chacun des acides aminés (ici, les fréquences d'apparition dans nos alignements de départ).


On en déduit la vraisemblance d'un alignement entre AAi et AAj : 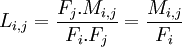L_{i,j} = \frac{F_j.M_{i,j}}{F_i.F_j} = \frac{M_{i,j}}{F_i}


En pratique, on utilise les logarithmes car 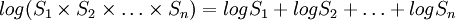log( S_1 \times S_2 \times \dots \times S_n ) = log S_1 + log S_2 + \dots + log S_n.


La matrice de substitution se calcule donc à l'aide de la formule suivante : 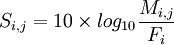S_{i,j} = 10 \times log_{10}\frac{M_{i,j}}{F_i}


Pour les fréquences de mutations de MM120 correspondant à 120 unités MM1, il faut multiplier 120 fois MM1 avec elle-même (produit vectoriel). 

round(MM120*100)
   A  R  N  D  C  Q  E  G  H  I  L  K  M  F  P  S  T  W  Y  V
A 33  3  5  4  7  6  5  4  3  4  3  5  5  2  4 11  6  1  2  6
R  2 31  4  2  2  6  3  1  4  1  1  9  2  1  1  3  3  1  1  1
N  2  3 38  5  2  4  3  2  4  1  1  4  2  1  1  5  3  1  2  1
D  3  2  8 32  1  5  9  2  4  1  1  4  1  1  2  5  3  1  1  1
C  1  0  1  0 30  0  0  0  0  1  0  0  1  1  0  1  1  1  1  1
Q  2  4  4  3  1 43  6  1  4  1  2  6  3  1  1  4  3  1  1  2
E  4  4  6 11  2 11 36  2  4  2  1  7  3  1  2  6  4  1  2  2
G  3  2  4  2  2  2  2 19  2  1  1  2  1  1  1  4  2  1  1  1
H  1  1  2  1  1  2  1  0 32  1  1  2  1  1  1  1  1  1  3  1
I  3  2  2  1  4  3  2  1  2 39  9  2 11  4  1  2  4  2  2 15
L  3  2  2  1  3  4  2  1  3 12 30  3 16  7  2  3  3  3  4  8
K  4 11  7  4  2 10  7  2  5  2  2 38  3  1  2  6  4  1  2  2
M  1  1  1  1  1  2  1  0  1  4  4  1 42  2  1  1  2  1  1  3
F  1  1  1  1  2  1  1  0  3  3  3  1  4 29  0  1  1  5  9  2
P  2  1  1  1  1  2  1  1  1  1  1  1  1  0 21  2  1  0  1  1
S  7  4  7  5  5  6  5  3  4  2  2  5  3  2  3 42  9  2  2  3
T  4  3  5  3  5  5  4  1  3  3  2  4  4  2  2  9 35  1  2  4
W  0  0  0  0  0  0  0  0  1  0  0  0  0  1  0  0  0 22  1  0
Y  1  1  1  1  1  1  1  0  4  1  1  1  2  6  0  1  1  4 28  1
V  5  2  2  1  7  4  2  1  2 17  7  3  9  4  2  4  6  2  2 38


Ensuite, il n'y a plus qu'à appliquer la formule 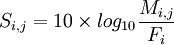S_{i,j} = 10 \times log_{10}\frac{M_{i,j}}{F_i}.

Vous devriez obtenir la matrice de substitution suivante : 

round(S120)
   A  R  N  D  C  Q  E   G  H   I   L  K  M   F   P  S  T   W   Y   V
A  6 -4 -3 -3 -1 -2 -2  -4 -4  -4  -4 -3 -3  -6  -3  1 -1  -8  -6  -2
R -4  8 -2 -4 -4  1 -2  -6 -2  -6  -6  2 -3  -7  -6 -2 -3  -7  -6  -6
N -2 -1 10  2 -3  0  0  -3  1  -5  -6  0 -4  -6  -5  1  0  -7  -3  -5
D -3 -4  1  7 -6  0  2  -5 -2  -8  -8 -2 -6  -9  -5 -1 -3  -9  -7  -7
C -1 -4 -3 -6 14 -5 -6  -7 -5  -3  -4 -5 -3  -3  -7  0 -1  -3  -3  -1
Q -1  1  1  0 -4 11  2  -5  1  -4  -3  2  0  -5  -3  1 -1  -5  -3  -3
E -2 -2  0  2 -6  2  7  -5 -2  -6  -7  0 -4  -8  -4 -1 -2  -8  -6  -5
G -4 -7 -3 -6 -7 -6 -6   3 -7 -11 -11 -6 -9 -12  -9 -4 -7 -11 -11 -10
H -4 -1  1 -2 -5  1 -2  -7 12  -6  -5 -1 -3  -2  -4 -2 -3  -2   1  -5
I -4 -6 -5 -8 -2 -4 -6 -10 -6   8   1 -5  2  -2  -8 -4 -2  -5  -4   4
L -5 -6 -6 -8 -4 -4 -7 -11 -5   1   5 -5  3  -1  -8 -5 -4  -6  -4   0
K -2  3  0 -2 -5  2  0  -5 -1  -5  -5  8 -3  -7  -4 -1 -2  -8  -5  -5
M -2 -3 -4 -6 -2  0 -4  -8 -2   2   3 -2 13   1  -6 -2 -1  -4  -2   1
F -6 -7 -6 -9 -3 -6 -8 -11 -2  -2  -1 -7  0   9  -9 -6 -6   1   3  -3
P -3 -6 -5 -6 -8 -4 -5  -9 -5  -8  -8 -5 -7 -10   7 -3 -5 -11  -9  -7
S  1 -2  1 -1  0  0 -1  -3 -2  -4  -4  0 -2  -5  -2  9  2  -5  -5  -3
T -1 -3  0 -3 -1 -1 -2  -6 -3  -2  -4 -2 -1  -5  -5  2  8  -8  -5  -1
W -9 -7 -7 -9 -4 -6 -9 -11 -3  -6  -6 -8 -5   0 -11 -6 -8  14   1  -6
Y -6 -6 -4 -7 -4 -4 -6 -11  1  -5  -4 -6 -3   3  -9 -5 -6   1  10  -5
V -2 -6 -5 -7 -1 -3 -5  -9 -5   3   0 -5  1  -3  -6 -3 -1  -6  -5   7


La matrice PAM1 est bien adaptée pour aligner des séquences dont la distance évolutive correspond au temps nécessaire pour qu'une mutation sur 100 a.a. soit fixée dans la population (PAM = Point Percent Accepted Mutation). En d'autres termes, chaque a.a. a une probabilité de 0.01 de muter. Pour apprécier la distance évolutive entre les séquences que nous avions au départ, nous allons calculer le pourcentage moyen de mutation d'un acide aminé. Vous devriez obtenir quelque chose comme 43,9%.

Retrieved from "http://silico.biotoul.fr/p/InfoBio_TD_Matrices_PAM"